In the exercise 9.2 of NCERT book for class 7, we are going to solve the questions on circumference of a circle, and area of a circle. A brief about these 2 –
Circle:
A circle is a two-dimensional geometric shape consisting of all points in a plane that are at a constant distance, called the radius, from a fixed point, known as the center.
Circumference of a Circle:
The circumference is the distance around the circle’s edge. It is calculated using the formula:
C = 2πr
or
C = πd
where ‘r’ is the radius of the circle, ‘d’ is the diameter (which is twice the radius, d = 2r), and ‘π’ (pi) is approximately equal to 3.14159.
Area of a Circle:
The area is the space enclosed within the circle. It is calculated using the formula:
A = πr²
where ‘r’ is the radius of the circle and ‘π’ is the mathematical constant pi.
Note: Pi (π) is a special number that represents the ratio of the circumference of any circle to its diameter.
Class 7 Maths Chapter 9 Perimeter and Area Exercise 9.2
Question 1: Find the circumference of the circles with the following radius: (Take π = 22/7)
(a) 14 cm (b) 28 mm (c) 21 cm
(a) Circumference when radius is 14 cm:
Circumference = 2 × π × radius
= 2 × (22/7) × 14 cm
= 2 × 22 × 2 cm
= 88 cm
(b) Circumference when radius is 28 mm:
Circumference = 2 × π × radius
= 2 × (22/7) × 28 mm
= 2 × 22 × 4 mm
= 176 mm
(c) Circumference when radius is 21 cm:
Circumference = 2 × π × radius
= 2 × (22/7) × 21 cm
= 2 × 22 × 3 cm
= 132 cm
Question 2: Find the area of the following circles, given that:
(a) radius = 14 mm (Take π = 22/7) (b) diameter = 49 m (c) radius = 5 cm
(a) Area when radius is 14 mm:
Area = π × radius²
= (22/7) × 14²
= (22/7) × 14 mm × 14 mm
= 22 × 2 × 14 mm² (14/7 = 2)
= 616 mm²
(b) Area when diameter is 49 m (radius is half the diameter, so 49/2 = 24.5 m):
Area = π × radius²
= (22/7) × 24.5 m × 24.5 m
= 22 × 24.5 × 3.5 (24.7/7 = 3.5)
= 22 × 85.75
= 1886.5 m²
(c) Area when radius is 5 cm:
Area = π × radius²
= (22/7) × 5 cm × 5 cm
= 22 × 5/7 × 5 cm²
= 110/7 × 5 cm²
= 550/7 cm²
= 78.57 cm²
Question 3: If the circumference of a circular sheet is 154 m, find its radius. Also, find the area of the sheet. (Take π = 22/7)
Step 1: Find the radius.
Circumference = 2 × π × radius
154 m = 2 × (22/7) × radius (putting the value of circumference = 154 m)
154 m = (44/7) × radius
Radius = (154 × 7)/44
Radius = 1078/44
Radius = 24.5 m
Step 2: Find the area using the radius.
Area = π × radius²
= (22/7) × 24.5 m × 24.5 m
= (22/7) × 600.25 m²
= 13205.7/7 m²
= 1886.5 m² (Ans)
The radius of the circular sheet is 24.5 meters, and the area is 1886.5 square meters.
Question 4: A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the cost of the rope, if it costs Rs. 4 per meter. (Take π = 22/7)
Step 1: Find the Circumference of the Garden
The circumference C of a circle is π times the diameter.
C = π × diameter
C = (22/7) × 21
C = 3 × 22
C = 66 m
Step 2: Calculate the Total Length of the Rope for 2 Rounds
Total length of rope needed = 2 × circumference of the garden
Total length of rope needed = 2 × 66
Total length of rope needed = 132 m
Step 3: Calculate the Cost of the Rope
Cost of the rope = total length of rope × cost per meter
Cost of the rope = 132 × 4
Cost of the rope = Rs. 528
The gardener needs to purchase 132 meters of rope, and the cost will be Rs. 528.
Question 5: From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)
Step 1: Find the Area of the Larger Sheet
The area A of the larger circle is π times radius squared.
A_larger = π × (radius of larger circle)²
A_larger = 3.14 × 4²
A_larger = 3.14 × 16
A_larger = 50.24 cm²
Step 2: Find the Area of the Smaller Circle
The area of the smaller circle A_smaller is π times radius squared.
A_smaller = π × (radius of smaller circle)²
A_smaller = 3.14 × 3²
A_smaller = 3.14 × 9
A_smaller = 28.26 cm²
Step 3: Find the Area of the Remaining Sheet
The area of the remaining sheet is the area of the larger circle minus the area of the smaller circle.
A_remaining = A_larger – A_smaller
A_remaining = 50.24 cm² – 28.26 cm²
A_remaining = 21.98 cm²
The area of the remaining sheet is 21.98 cm².
Question 6: Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs Rs. 15. (Take π = 3.14)
Step 1: Find the Circumference of the Table Cover
Circumference C = π × diameter
C = 3.14 × 1.5
C = 4.71 m
Step 2: Calculate the Cost of the Lace
Cost of lace = circumference × cost per meter
Cost of lace = 4.71 × 15
Cost of lace = Rs. 70.65
Saima will need 4.71 meters of lace, and the cost will be Rs. 70.65.
Question 7: Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
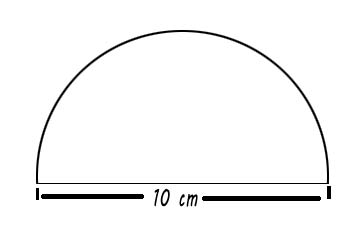
Solution:
To find the perimeter of the semicircle including its diameter, we need to calculate the length of the semicircle’s arc and then add the length of the diameter.
The formula for the circumference of a full circle is C = 2 × π × r, where r is the radius. For a semicircle, the arc length will be half of this, plus the diameter.
Given the diameter is 10 cm, the radius r will be half of that, which is 5 cm.
Perimeter of the semicircle = π × r + diameter
= π × 5 + 10
= 5π + 10 centimeter
Perimeter = 5 × 3.14 + 10
= 15.7 + 10
= 25.7 cm
Keep π in its exact form, or use an approximation? The choice depends on the level of precision required.
Question 8: Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is Rs. 15/m². (Take π = 3.14).
Step 1: Find the Area of the Table-Top
The radius of the table-top is half of the diameter, so the radius is 1.6 / 2 = 0.8 m. The area A is:
A = π × r²
A = 3.14 × 0.8²
A = 3.14 × 0.64
A = 2.0096 m²
Step 2: Calculate the Polishing Cost
Cost = Area × Rate of polishing
Cost = 2.0096 m² × 15 Rs/m²
Cost = Rs. 30.144
The cost of polishing the table-top is Rs. 30.144.
Question 9: Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (Take π = 22/7).
Step 1: Find the Radius of the Circle
The circumference of the circle is equal to the length of the wire. So, using C = 2 × π × r:
44 = 2 × (22/7) × r
r = 44 / (2 × (22/7))
r = 44 / (44/7)
r = 7 cm
Step 2: Find the Area of the Circle
A = π × r²
A = (22/7) × 7²
A = (22/7) × 49
A = 22 × 7
A = 154 cm²
Step 3: Find the Length of Each Side of the Square
The perimeter of the square is equal to the length of the wire. For a square, P = 4 × side:
44 = 4 × side
side = 44 / 4
side = 11 cm
Step 4: Find the Area of the Square
Area of square = side²
Area of square = 11²
Area of square = 121 cm²
Step 5: Determine Which Shape Encloses More Area
The circle encloses more area (154 cm²) than the square (121 cm²).
The circle has a radius of 7 cm and an area of 154 cm². The square has sides of length 11 cm and an area of 121 cm². The circle encloses more area.
Question 10: From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed. Find the area of the remaining sheet. (Take π = 22/7).
Step 1: Find the Area of the Large Circle
A_large = π × r²
A_large = (22/7) × 14²
A_large = (22/7) × 196
A_large = 22 × 28
A_large = 616 cm²
Step 2: Find the Area of the Small Circles
Each small circle has an area of:
A_small = π × r²
A_small = (22/7) × 3.5²
A_small = (22/7) × 12.25
A_small = 22 × 1.75
A_small = 38.5 cm²
The total area of the two small circles is:
Total_A_small = 2 × 38.5
Total_A_small = 77 cm²
Step 3: Find the Area of the Rectangle
A_rectangle = length × breadth
A_rectangle = 3 × 1
A_rectangle = 3 cm²
Step 4: Calculate the Remaining Area
Remaining_area = A_large – Total_A_small – A_rectangle
Remaining_area = 616 – 77 – 3
Remaining_area = 536 cm²
The area of the remaining sheet is 536 cm².
Question 11: A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left-over aluminium sheet? (Take π = 3.14).
Step 1: Find the Area of the Square
The area of the square A_square is calculated as side times side.
A_square = 6 cm × 6 cm
A_square = 36 cm²
Step 2: Find the Area of the Circle
The area of the circle A_circle is calculated using the formula π times r squared.
A_circle = 3.14 × 2 cm × 2 cm
A_circle = 3.14 × 4 cm²
A_circle = 12.56 cm²
Step 3: Calculate the Remaining Area
The remaining area of the aluminium sheet A_remaining is the area of the square minus the area of the circle that was cut out.
A_remaining = A_square – A_circle
A_remaining = 36 cm² – 12.56 cm²
A_remaining = 23.44 cm²
The area of the left-over aluminium sheet is 23.44 cm².
Question 12: The circumference of a circle is 31.4 cm. Find the radius and the area of the circle (Take π = 3.14).
Step 1: Find the Radius
The formula for the circumference of a circle is C = 2 × π × r. We have C = 31.4 cm, so we can solve for r (radius):
31.4 = 2 × 3.14 × r
r = 31.4 / (2 × 3.14)
r = 31.4 / 6.28
r = 5 cm
Step 2: Find the Area
The area A of a circle is A = π × r². Using r = 5 cm:
A = 3.14 × 5²
A = 3.14 × 25
A = 78.5 cm²
The radius is 5 cm and the area is 78.5 cm².
Question 13: A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14).
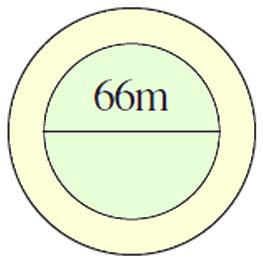
Step 1: Find the Area of the Flower Bed
The radius of the flower bed is half of the diameter, so the radius is 66 / 2 = 33 m. The area A1 is:
A1 = π × r²
A1 = 3.14 × 33²
A1 = 3.14 × 1089
A1 = 3419.46 m²
Step 2: Find the Area of the Flower Bed with Path
The overall radius including the path is 33 m + 4 m = 37 m. The total area A2 is:
A2 = π × R²
A2 = 3.14 × 37²
A2 = 3.14 × 1369
A2 = 4298.66 m²
Step 3: Find the Area of the Path
Area of the path = A2 – A1
Area of the path = 4298.66 m² – 3419.46 m²
Area of the path = 874.6 m²
The area of the path is 879.20 m².
Question 14: A circular flower garden has an area of 314 m². A sprinkler at the center of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take π = 3.14).
Step 1: Find the Area Covered by the Sprinkler
The area As the sprinkler can cover is As = π × r² with r = 12 m:
As = 3.14 × 12²
As = 3.14 × 144
As = 452.16 m²
Step 2: Compare the Areas
If As (area sprinkler can cover) ≥ Area of the garden, the sprinkler will water the entire garden.
452.16 m² is greater than 314 m², so the sprinkler will water the entire garden.
Question 15: Find the circumference of the inner and the outer circles, shown in the adjoining figure? (Take π = 3.14)
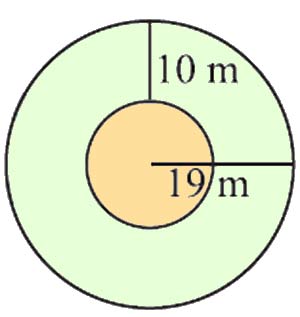
To find the circumference of the inner and outer circles, we will use the formula C = 2 × π × r.
The Radius of the outer circle in the diagram above is 19 m. As we can see, the distance between the inner circle and outer circle is 10 m.
Therefore radius of the inner circle = 19 m – 10 m = 9 m
For the inner circle with a radius of 9 m:
Circumference of the inner circle = 2 × π × 9
= 2 × 3.14 × 9
= 56.52 m
For the outer circle with a radius of 19 m :
Circumference of the outer circle = 2 × π × 19
= 2 × 3.14 × 19
= 119.32 m
Therefore, the circumference of the inner circle is 56.52 m, and the circumference of the outer circle is 119.32 m
Question 16: How many times a wheel of radius 28 cm must rotate to go 352 m? (Take π = 22/7)
Step 1: Find the Circumference of the Wheel
The formula for the circumference is 2 × π × radius. Using the radius of 28 cm:
Circumference = 2 × (22/7) × 28 cm
Circumference = 2 × 22 × 4 cm
Circumference = 176 cm
Step 2: Convert the Distance to Centimeters
The distance the wheel needs to cover is 352 m. Convert this to centimeters:
352 m = 352 × 100 cm
352 m = 35200 cm
Step 3: Calculate the Number of Rotations
The number of rotations is the total distance to cover divided by the circumference of the wheel:
Number of rotations = Total distance in cm / Circumference
Number of rotations = 35200 cm / 176 cm
Number of rotations = 200
So the wheel must rotate 200 times to cover 352 meters.
Question 17: The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour. (Take π = 3.14)
Step 1: Find the Circumference of the Circle
The formula for the circumference (C) is 2 × π × radius (r). The radius in this case is the length of the minute hand, which is 15 cm:
C = 2 × π × r
C = 2 × 3.14 × 15 cm
Now calculate the circumference:
C = 2 × 3.14 × 15
C = 6.28 × 15
C = 94.2 cm
Step 2: Calculate the Distance for 1 Hour
In 1 hour, the minute hand completes one full rotation. The distance the tip of the minute hand moves is equal to the circumference of the circle it traces:
Distance moved in 1 hour = Circumference of the circle
Distance moved in 1 hour = 94.2 cm
So, the tip of the minute hand moves 94.2 cm in 1 hour.
Extra Challenging MCQ Questions for Perimeter and Area Exercise 9.2
1. A circular garden has a circumference of 44 meters. What is its area? (Use π = 22/7)
a) 154 m²
b) 308 m²
c) 616 m²
d) 77 m²
Answer:
a) 154 m²
2. If the radius of a circle is tripled, how does its area change?
a) It doubles
b) It triples
c) It becomes nine times larger
d) It remains the same
Answer:
c) It becomes nine times larger
3. The area of a circle is 616 cm². What is its diameter? (Use π = 22/7)
a) 14 cm
b) 28 cm
c) 21 cm
d) 42 cm
Answer:
b) 28 cm
4. A wire is bent into the shape of a circle with a radius of 7 cm. If the same wire is bent into a square, what will be the length of each side? (Use π = 22/7)
a) 11 cm
b) 22 cm
c) 14 cm
d) 28 cm
Answer:
a) 11 cm
5. The ratio of the areas of two circles is 1:4. What is the ratio of their circumferences?
a) 1:2
b) 1:4
c) 1:8
d) 1:16
Answer:
a) 1:2
6. A circular track has a diameter of 70 meters. How many complete rounds must a runner make to cover 1 kilometer? (Use π = 22/7)
a) 2
b) 3
c) 4
d) 5
Answer:
c) 4
7. The area of a semicircle is 77 cm². What is its perimeter? (Use π = 22/7)
a) 28 cm
b) 36 cm
c) 44 cm
d) 56 cm
Answer:
b) 36 cm
8. A circular ring has an outer radius of 14 cm and an inner radius of 7 cm. What is the area of the ring? (Use π = 22/7)
a) 154 cm²
b) 462 cm²
c) 308 cm²
d) 616 cm²
Answer:
a) 154 cm²
9. The circumference of a circle is equal to the perimeter of a square. If the side of the square is 11 cm, what is the radius of the circle? (Use π = 22/7)
a) 7 cm
b) 14 cm
c) 21 cm
d) 28 cm
Answer:
a) 7 cm
10. A sector of a circle has an angle of 90° and a radius of 14 cm. What is the area of the sector? (Use π = 22/7)
a) 77 cm²
b) 154 cm²
c) 308 cm²
d) 616 cm²
Answer:
a) 77 cm²
Worksheet: Perimeter and Area Exercise 9.2
Questions
- Find the area of a rectangular park with dimensions 180 m by 120 m.
- What is the length of a side of a square with an area of 484 m²?
- The perimeter of a rectangular plot is 350 m. If its length is 100 m, determine its width.
- A rectangular area measures 80 m in length and 60 m in width. Calculate its total area.
- Identify the length of a square’s side if its perimeter is the same as that of a 50 m by 30 m rectangle.
- If a square field has a perimeter of 360 m, find out its area.
- What is the perimeter of a rectangular garden that is 40 m long and 25 m wide?
- A rectangle and a square have the same perimeter. If the side of the square is 30 m and the length of the rectangle is 34 m, what is the rectangle’s width?
- The length of a rectangular field is four times its width. If the field’s area is 256 m², find its dimensions.
- Calculate the perimeter of a square plot with an area of 1600 m².
- Estimate the width of a rectangle with a perimeter of 220 m and a length of 70 m.
- Compute the area of a square land parcel with sides measuring 70 m.
- Given a rectangular park that is three times as long as it is broad, with an area of 675 m², determine its length and width.
- Suppose a rectangular lawn’s length is extended by 10 m and its width is reduced by 10 m, with the area staying constant at 600 m². If the original length is 30 m, find its new dimensions.
- If the diagonal of a rectangle measures 30 m and the width is 18 m, calculate the rectangle’s length and the perimeter.
Answers
- Area = 180 m × 120 m = 21,600 m²
- Side = sqrt(484 m²) = 22 m
- Width = (350 m – 2 × 100 m)/2 = 75 m
- Area = 80 m × 60 m = 4,800 m²
- Side of square = Perimeter of rectangle / 4 = (2 × (50 m + 30 m)) / 4 = 40 m
- Area = (360 m / 4)² = 8,100 m²
- Perimeter = 2 × (40 m + 25 m) = 130 m
- Width of rectangle = (Perimeter of square – 2 × Length of rectangle) / 2 = (4 × 30 m – 2 × 34 m) / 2 = 26 m
- Width = sqrt(256 m²/4), Length = 4 × Width
- Perimeter = 4 × sqrt(1600 m²) = 160 m
- Width = (220 m – 2 × 70 m) / 2 = 40 m
- Area = 70 m × 70 m = 4,900 m²
- Width = sqrt(675 m²/3), Length = 3 × Width
- New dimensions: Length = 30 m + 10 m, Width = sqrt(600 m² / New Length)
- Length = sqrt(30 m² – 18 m²), Perimeter = 2 × (Length + 18 m)