Let’s check some of the things we will cover in the solutions for Exercise 9.3 in Mensuration Chapter 9. Here we are going to cover –
- Volume of Cube, Cuboid, and Cylinder
- Volume and Capacity
Volume of Cube, Cuboid and Cylinder
Volume
Volume is the measure of the space occupied by a three-dimensional object. It is expressed in cubic units.
Capacity
Capacity refers to the amount of substance (like liquid or gas) a container can hold. It’s often measured in liters or milliliters.
Volume of a Cube
The Volume of a cube is calculated by cubing the length of its side.
Volume = side³
For example, if each side of a cube is 3 cm, the Volume is 3³ = 27 cm³.
Volume of a Cuboid
A cuboid is a three-dimensional figure with six rectangular faces. The volume formula considers the three dimensions: length (l), breadth (b), and height (h). The formula, Volume = l × b × h, multiplies these dimensions. It measures the total space inside the cuboid.
Volume = length × breadth × height
If a cuboid has a length of 4 cm, breadth of 3 cm, and height of 2 cm, its Volume is 4 × 3 × 2 = 24 cm³.
Volume of a Cylinder
The Volume of a cylinder is calculated by considering its circular base and height. The area of the circular base is given by π times the radius squared (πr²), where ‘r’ is the radius of the circular base. This formula calculates the space inside the cylinder from the circular base throughout its height.
Volume = π × radius² × height
If the cylinder, for example, has a radius of 2 cm and a height of 5 cm, its Volume is π × 2² × 5 = 20π cm³ (62.83 cm³).
NCERT Solutions for Class 8 Maths Exercise 9.3 Chapter 9 Mensuration
1. Given a cylindrical tank, in which situation will you find surface area and in which situation volume.
(a) To find how much it can hold.
Volume (because volume measures the capacity of the tank).
(b) Number of cement bags required to plaster it.
Surface Area (because plastering involves covering the surface).
(c) To find the number of smaller tanks that can be filled with water from it.
Volume (as it’s a matter of the tank’s capacity).
2. Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?
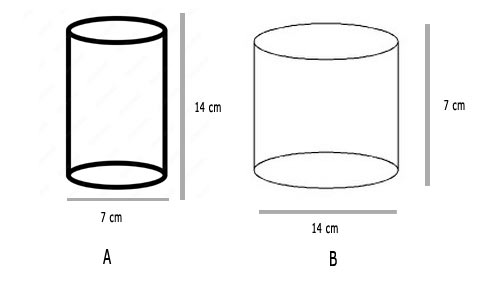
Since the diameter of cylinder B is greater(double) than that of A, we can say that the volume of the cylinder B will be greater without performing any calculations.
Let’s verify this by calculating the volume of both cylinders:
For cylinder A:
Radius r = diameter / 2 = 7 cm / 2 = 3.5 cm
Height of cylinder A: h = 14 cm
Volume V = π * r² * h = (22/7) * (3.5 cm)² * 14 cm
Volume V = (22/7) * 12.25 cm² * 14 cm
Volume V = 22 * 12.25 cm² * 2 cm (dividing numerator 14 by denominator 7)
Volume V = 539 cm³
For cylinder B:
Radius r = diameter / 2 = 14 cm / 2 = 7 cm
Height of cylinder B: h = 7 cm
Volume V = π * r² * h = (22/7) * (7 cm)² * 7 cm
Volume V = (22/7) * 49 cm² * 7 cm
Volume V = 22 * 7 cm * 7 cm
Volume V = 1078 cm³
From the calculation, we have verified that the volume of the cylinder B is greater.
Surface area comparison:
For cylinder A:
Surface area A = 2 * π * r (h + r)
A = 2 * (22/7) * 3.5 cm (14 + 3.5)
A = 22 *(28 + 7)/2
A = (22 * 35)/2
A = 385 cm²
For cylinder B:
Surface area A = 2 * π * r (h + r)
A = 2 * (22/7) * 7 cm (7 + 7)
A = 2 * (22/7) * 7 cm (14)
A = 44 * 14
A = 616 cm²
Cylinder B has a greater surface area of 616 cm² compared to cylinder A’s surface area of 385 cm².
Question 3: Find the height of a cuboid whose base area is 180 cm² and volume is 900 cm³.
Formula for volume of a cuboid: Volume = Base Area × Height
Given: Volume = 900 cm³, Base Area = 180 cm²
Volume = Base Area × Height
Height = Volume / Base Area
Height = 900 cm³ / 180 cm² = 5 cm
The height of cuboid is 5 cm
Question 4: A cuboid is of dimensions 60 cm × 54 cm × 30 cm. How many small cubes with side 6 cm can be placed in the given cuboid?
Given, dimensions of cuboid = 60 cm × 54 cm × 30 cm
Length = 60 cm
Width = 54 cm
Height = 30 cm
Formula for volume of the cuboid = Length × Width × Height
= 60 cm × 54 cm × 30 cm = 97200 cm³
Given side of small cube is 6 cm
Volume of a small cube = Side³
= 6 cm × 6 cm × 6 cm = 216 cm³
Since small cubes are placed in the given cuboid –
Number of small cubes = Volume of the cuboid / Volume of a cube
= 97200 cm³ / 216 cm³ = 450
Question 5: Find the height of the cylinder whose volume is 1.54 m³ and diameter of the base is 140 cm.
Radius of the base = Diameter / 2
= 140 cm / 2 = 70 cm = 0.7 m (since 1m = 100cm)
Formula for volume of a cylinder: Volume = π × r² × Height
Given: Volume = 1.54 m³, r = 0.7 m
Height = Volume / (π × r²)
= 1.54 m³ / (π × 0.7 m × 0.7 m)
Height = 1 m (using π = 3.14)
Question 6: A milk tank is in the form of a cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in liters that can be stored in the tank.

Radius of the cylindrical tank = 1.5 m (given)
Height of the cylindrical tank = 7m
Formula for volume of a cylinder: Volume = π × r² × Height
Given: r = 1.5 m, Height (length of the tank) = 7 m
Volume = π × 1.5 m × 1.5 m × 7 m
Volume = (22/7) × 1.5 m × 1.5 m × 7 m
Volume = 49.5 m³ (using π = 22/7)
Since 1 m³ = 1000 L
Volume = 49.5 * 1000
= 49500 L
Question 7: If each edge of a cube is doubled, (i) how many times will its surface area increase? (ii) how many times will its volume increase?
(i) Increase in Surface Area:
The formula for the surface area of a cube is 6 × (edge length)². Let’s say the original edge length is ‘a’. So, the original surface area is 6a².
When the edge length is doubled, the new edge length becomes 2a. The new surface area is then 6 × (2a)² = 6 × 4a² = 24a².
To find how many times the surface area increases, we divide the new surface area by the original surface area.
So, it increases by a factor of 24a² / 6a² = 4 times.
(ii) Increase in Volume:
The formula for the volume of a cube is (edge length)³. The original volume is a³.
When the edge length is doubled to 2a, the new volume becomes (2a)³ = 8a³.
To find how many times the volume increases, we divide the new volume by the original volume.
So, it increases by a factor of 8a³ / a³ = 8 times.
Question 8: Water is pouring into a cuboidal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108 m3, find the number of hours it will take to fill the reservoir.
Finding the Time to Fill the Reservoir:
We are given the rate of water flow as 60 liters per minute and the volume of the reservoir as 108 m³.
First, we need to convert the volume of the reservoir from cubic meters to liters, because the flow rate is in liters. 1 m³ = 1000 liters.
So, the volume of the reservoir is 108 × 1000 = 108,000 liters.
Now, we find the time taken to fill the reservoir. Time = Volume / Rate.
So, the time taken to fill the reservoir is 108,000 liters / 60 liters per minute = 1800 minutes.
To convert minutes into hours, we divide by 60. Thus, 1800 minutes / 60 = 30 hours.
So, it will take 30 hours to fill the reservoir.
Additional Questions for Exercise 9.3 Chapter 9 Mensuration
Question 1: Calculate the height of a cylinder with a base area of 250 cm² and a volume of 1,250 cm³.
Solution:
Base area = 250 cm²
Volume = 1,250 cm³
Height = Volume / Base Area
Height = 1,250 / 250
Height = 5 cm
Question 2: A tank in the shape of a rectangular prism measures 80 cm × 50 cm × 40 cm. How many cubes of 10 cm side can fit inside the tank?
Solution:
Volume of the tank = 80 x 50 x 40 = 160,000 cm³
Volume of one cube = 10 x 10 x 10 = 1,000 cm³
Number of cubes = Volume of the tank / Volume of one cube
Number of cubes = 160,000 / 1,000
Number of cubes = 160
Question 3: Find the radius of a sphere whose volume is 1,436 cm³.
Solution:
Volume of a sphere = 4/3 πr³
1,436 = 4/3 πr³
r³ = (1,436 x 3)/4PII
r³ = 343.91
r = 7 cm (Approximately, using π = 3.14)
Question 4: A conical flask has a volume of 1,232 cm³ and a radius of 7 cm. Find the height of the cone.
Solution:
Volume of a cone = 1/3 πr²h
1,232 = 1/3 × π × 7² x h
h = (1232 × 3)/(π × 49)
h = 24 cm (Using π = 3.14)
Question 5: Calculate the total surface area of a hemispherical bowl of radius 5 cm.
Solution:
Radius (r) = 5 cm
Total surface area of a hemisphere = 3πr²
Total surface area = 3 x π x 5²
Total surface area = 3 x π x 25
Total surface area ≈ 235.5 cm² (Approximately, using π = 3.14)
Extra MCQ Questions for Class 8 Chapter 9 Mensuration
1. What is the formula for the volume of a cube with side length ‘a’?
- a) a²
- b) 4a
- c) a³
- d) 6a²
Answer:
c) a³
2. If the radius of a cylinder is doubled and the height remains the same, how does the volume change?
- a) It remains the same
- b) It doubles
- c) It triples
- d) It quadruples
Answer:
d) It quadruples
3. The surface area of a cuboid is given by which formula?
- a) 2(lb + bh + hl)
- b) l + b + h
- c) lbh
- d) 4πr²
Answer:
a) 2(lb + bh + hl)
4. A cylindrical tank has a radius of 7 cm and a height of 10 cm. What is its volume? (Use π = 22/7)
- a) 1540 cm³
- b) 440 cm³
- c) 154 cm³
- d) 3080 cm³
Answer:
a) 1540 cm³
5. Which of the following shapes has the largest volume if all have the same surface area?
- a) Cube
- b) Sphere
- c) Cylinder
- d) Cone
Answer:
b) Sphere
6. The capacity of a container is measured in:
- a) Square units
- b) Cubic units
- c) Linear units
- d) None of the above
Answer:
b) Cubic units
7. If the height of a cylinder is halved while keeping the radius constant, how does the volume change?
- a) It remains the same
- b) It doubles
- c) It halves
- d) It quadruples
Answer:
c) It halves
8. The lateral surface area of a cylinder is given by which formula?
- a) 2πrh
- b) πr²h
- c) 2πr(h + r)
- d) πr²
Answer:
a) 2πrh
9. A cube has a volume of 64 cm³. What is the length of each side?
- a) 2 cm
- b) 4 cm
- c) 8 cm
- d) 16 cm
Answer:
b) 4 cm
10. If the side length of a cube is tripled, how does its volume change?
- a) It remains the same
- b) It triples
- c) It increases nine times
- d) It increases twenty-seven times
Answer:
d) It increases twenty-seven times