Let’s solve the 10.3 exercise in chapter 10, Mensuration of NCERT book for Class 6. This is the last exercise, where we will solve questions on the Area of a Rectangle and the Area of a Square.
Essential concepts for solving Mensuration Exercise 10.3 of Chapter 10
Area of a Rectangle
Formula: Area = Length × Width
Explanation: The area of a rectangle is calculated by multiplying its length by its width.
Example: If a rectangle has a length of 10 meters and a width of 5 meters, its area is 10 meters × 5 meters = 50 square meters or 50 m²
Area of a Square
Formula: Area = Side × Side (or Side²)
Explanation: Since all sides of a square are equal, the area is found by multiplying the length of one side by itself.
Example: If a square has sides of 6 meters, its area is 6 meters × 6 meters = 36 square meters or 36 m²
NCERT Solutions for Class 6 Maths Exercise 10.3 Chapter 10 Mensuration
1. Find the areas of the rectangles whose sides are:
(a) 3 cm and 4 cm (b) 12 m and 21 m (c) 2 km and 3 km (d) 2 m and 70 cm
Solution:
The area of a rectangle is calculated by multiplying its length by its breadth.
(a) For a rectangle with sides 3 cm and 4 cm:
Area = Length × Breadth = 3 cm × 4 cm = 12 cm²
(b) For a rectangle with sides 12 m and 21 m:
Area = 12 m × 21 m = 252 m²
(c) For a rectangle with sides 2 km and 3 km:
Area = 2 km × 3 km = 6 km²
(Note: 1 km = 1000 m, so the area can also be expressed as 6,000,000 m²)
(d) For a rectangle with sides 2 m and 70 cm:
First, convert 70 cm to meters. 1 m = 100 cm, so 70 cm = 0.7 m.
Area = 2 m × 0.7 m = 1.4 m²
2. Find the areas of the squares whose sides are :
(a) 10 cm (b) 14 cm (c) 5 m
Solution:
The area of a square is calculated by squaring its side length.
(a) For a square with a side of 10 cm:
Area = Side × Side = 10 cm × 10 cm = 100 cm²
(b) For a square with a side of 14 cm:
Area = 14 cm × 14 cm = 196 cm²
(c) For a square with a side of 5 m:
Area = 5 m × 5 m = 25 m²
3. The length and breadth of three rectangles are as given below :
(a) 9 m and 6 m (b) 17 m and 3 m (c) 4 m and 14 m
Which one has the largest area and which one has the smallest?
Solution:
Calculate the area of each rectangle and compare.
(a) Area of rectangle 9 m x 6 m:
Area = 9 m × 6 m = 54 m²
(b) Area of rectangle 17 m x 3 m:
Area = 17 m × 3 m = 51 m²
(c) Area of rectangle 4 m x 14 m:
Area = 4 m × 14 m = 56 m²
The rectangle with the largest area is (c) 4 m x 14 m with 56 m², and the smallest is (b) 17 m x 3 m with 51 m².
4. The area of a rectangular garden 50 m long is 300 sq m. Find the width of the garden.
Solution:
To find the width, we use the formula for the area of a rectangle: Area = Length × Width.
Given:
Length = 50 m
Area = 300 m²
We rearrange the formula to solve for Width: Width = Area / Length.
So, the width of the garden is:
Width = 300 m² / 50 m = 6 m.
Therefore, the width of the garden is 6 meters.
5. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ` 8 per hundred sq m.?
Solution:
First, calculate the area of the land, and then determine the cost based on the given rate.
Area = Length × Width = 500 m × 200 m = 100,000 m²
Now, calculate the cost. The rate is ₹ 8 per hundred square meters.
Total number of hundred square meters in 100,000 m² = 100,000 / 100 = 1,000
Cost = 1,000 × ₹ 8 = ₹ 8,000
Thus, the cost of tiling the land is ₹ 8,000.
6. A table-top measures 2 m by 1 m 50 cm. What is its area in square metres?
Solution:
First, convert all measurements to meters. 1 m 50 cm = 1.5 m.
Length of table-top = 2 m
Width of table-top = 1.5 m
Area = Length × Width = 2 m × 1.5 m = 3 m²
The area of the table-top is 3 square metres.
7. A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?
Solution:
Convert 3 m 50 cm to meters: 3.5 m.
Length of the room = 4 m
Width of the room = 3.5 m
Area = Length × Width = 4 m × 3.5 m = 14 m²
14 square metres of carpet is needed to cover the floor.
8. A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solution:
Calculate the area of the floor and the area of the carpet, then subtract.
Area of floor = Length × Width = 5 m × 4 m = 20 m²
Area of carpet = Side² = 3 m × 3 m = 9 m²
Area not carpeted = Area of floor – Area of carpet = 20 m² – 9 m² = 11 m²
The area not carpeted is 11 square metres.
9. Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
Solution:
First, calculate the area of the land and then the total area of the flower beds.
Area of land = Length × Width = 5 m × 4 m = 20 m²
Area of one flower bed = Side² = 1 m × 1 m = 1 m²
Total area of five flower beds = 1 m² × 5 = 5 m²
Remaining area = Area of land – Total area of flower beds = 20 m² – 5 m² = 15 m²
The area of the remaining part of the land is 15 square metres.
11. Split the following shapes into rectangles and find their areas. (The measures are given in centimetres)
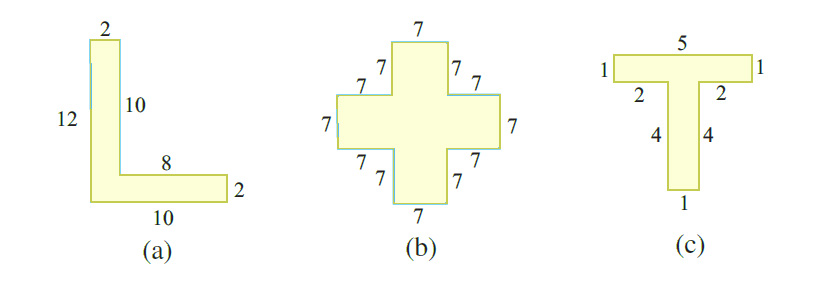
Solution:
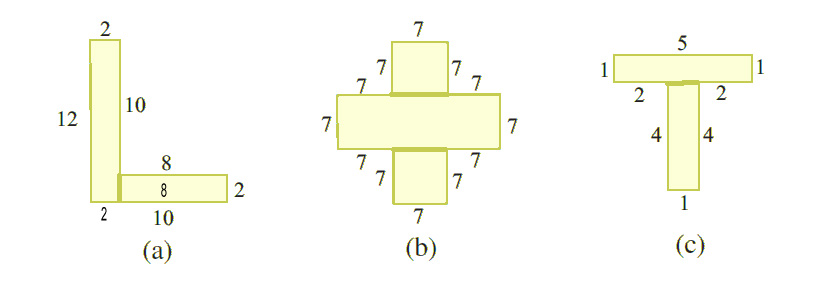
Shape (a):
Break it into two rectangles.
Rectangle 1 (Vertical): 12 cm by 2 cm.
Rectangle 2 (Horizontal): 2 cm by 8 cm.
Areas:
Area of Rectangle 1 = Length × Width = 12 cm × 2 cm = 24 cm².
Area of Rectangle 2 = Length × Width = 2 cm × 8 cm = 16 cm².
Total Area of Shape (a) = Area of Rectangle 1 + Area of Rectangle 2 = 24 cm² + 16 cm² = 40 cm².
Shape (b):
Break it into three rectangles.
Rectangle 1 (Center): 7 cm by 7 cm.
Rectangle 2 (Top): 7 cm by 7 cm.
Rectangle 3 (Bottom): 7 cm by 7 cm.
Areas:
Area of Rectangle 1 = 7 cm × 7 cm = 49 cm².
Area of Rectangle 2 = 21 cm × 7 cm = 147 cm².
Area of Rectangle 3 = 7 cm × 7 cm = 49 cm².
Total Area of Shape (b) = Area of Rectangle 1 + Area of Rectangle 2 + Area of Rectangle 3 = 49 cm² + 147 cm² + 49 cm² = 245 cm².
Shape (c):
Break it into two rectangles.
Rectangle 1 (Top): 5 cm by 1 cm.
Rectangle 2 (Vertical): 4 cm by 1 cm.
Areas:
Area of Rectangle 1 = 5 cm × 1 cm = 5 cm².
Area of Rectangle 2 = 4 cm × 1 cm = 4 cm².
Total Area of Shape (c) = Area of Rectangle 1 + Area of Rectangle 2 = 5 cm² + 4 cm² = 9 cm².
12. How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively:
(a) 100 cm and 144 cm (b) 70 cm and 36 cm.
Solution:
First, calculate the area of a single tile and then the area of each rectangular region. Divide the area of the region by the area of a tile to find the number of tiles needed.
For (a) 100 cm and 144 cm
Area of a tile:
Area = Length × Breadth = 12 cm × 5 cm = 60 cm²
Area of the rectangular region:
Area = Length × Breadth = 100 cm × 144 cm = 14,400 cm²
Number of tiles needed:
Number of tiles = Area of region / Area of a tile = 14,400 cm² / 60 cm² = 240
240 tiles are needed for the rectangular region measuring 100 cm by 144 cm.
For (b) 70 cm and 36 cm
Area of the rectangular region:
Area = Length × Breadth = 70 cm × 36 cm = 2,520 cm²
Number of tiles needed: (using the same area of a tile as in (a))
Number of tiles = Area of region / Area of a tile = 2,520 cm² / 60 cm² ≈ 42
Approximately 42 tiles are needed for the rectangular region measuring 70 cm by 36 cm.
Additional Worksheet Questions for Exercise 10.3 Mensuration for Class 6
Answers
- 37.5 sq cm
- 48 sq m
- 576 sq cm
- 50 sq cm
- 30 m
- 51 sq m
- 25.42 sq m
- 25 sq m
- 250 sq m
- 99 sq cm
- 800 sq m
- 196 sq cm