NCERT Solutions for Class 8 Maths Exercise 3.4 Chapter 3 Understanding Quadrilaterals
1. State whether True or False.
Solution:
(a) All rectangles are squares
False.
While all squares are rectangles (due to having 4 right angles), not all rectangles are squares because rectangles have sides of different lengths.
(b) All rhombuses are parallelograms
True.
All rhombuses are parallelograms because they have opposite sides, parallel and equal length.
(c) All squares are rhombuses and also rectangles
True.
All squares are rhombuses (due to all sides being equal) and also rectangles (due to all angles being right angles).
(d) All squares are not parallelograms.
False.
All squares are parallelograms because they have both pairs of opposite sides parallel.
(e) All kites are rhombuses.
False.
Not all kites are rhombuses. Kites have two pairs of equal adjacent sides, but rhombuses have all sides equal.
(f) All rhombuses are kites.
False.
Not all rhombuses are kites. Rhombuses have all sides and opposite angles equal, which is not required for kites.
(g) All parallelograms are trapeziums.
True.
All parallelograms are trapeziums (trapezoids in American English) because a trapezium is defined as a quadrilateral with at least one pair of parallel sides, and parallelograms have two pairs.
(h) All squares are trapeziums.
True.
All squares are trapeziums because squares have two pairs of parallel sides, fitting the definition of a trapezium.
2. Identify all the quadrilaterals that have.
Solution:
(a) four sides of equal length
Four sides of equal length: Square, Rhombus. Both quadrilaterals have four sides of equal length by definition.
(b) four right angles
Four right angles: Square, Rectangle. Both have four right angles by definition.
3. Explain how a square is.
Solution:
(i) a quadrilateral:
A square has four sides, which makes it a quadrilateral. A quadrilateral is a four-sided polygon.
(ii) a parallelogram:
A square has both pairs of opposite sides parallel and equal in length. These characteristics meet the criteria of a parallelogram.
(iii) a rhombus:
A square has all four sides of equal length. This is a defining characteristic of a rhombus.
(iv) a rectangle:
A square has four right angles. It is one of the primary characteristics of a rectangle.
4. Name the quadrilaterals whose diagonals.
Solution:
i) bisect each other
Parallelogram, Rectangle, Rhombus, Square. The diagonals of these quadrilaterals bisect each other into two equal parts.
(ii) are perpendicular bisectors of each other:
Rhombus, Square. The diagonals of these quadrilaterals are perpendicular to each other. Each diagonal bisects the other.
(iii) are equal:
Rectangle, Square. The diagonals of these quadrilaterals are equal in length.
5. Explain why a rectangle is a convex quadrilateral.
Solution:
A rectangle is a convex quadrilateral because all its interior angles are less than 180 degrees. It also meets the other criteria as the line segment between any two points within the rectangle lies entirely inside it.
6. ABC is a right-angled triangle, and O is the side’s midpoint opposite the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).
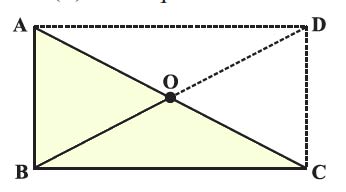
Solution:
Since triangle ABC is a right-angled triangle, the side opposite the right angle (hypotenuse AC) is the longest side. Point O is the midpoint of AC.
It means AO = OC.
Because O is the midpoint, two smaller triangles, AOB and COB, are formed within the larger triangle ABC.
These two triangles are congruent to each other by the Side-Angle-Side (SAS) postulate:
1. AO = OC (O is the midpoint of AC).
2. Angle AOB equals angle COB (each being 90 degrees since they are angles on a straight line, which adds up to 180 degrees).
3. OB is common to both triangles AOB and COB.
Since triangles AOB and COB are congruent, their corresponding sides are equal, so we also have OB = OB (common side) and AB = CB (by the Pythagorean theorem in triangle ABC).
Therefore, point O is equidistant from A, B, and C, as OA = OC and OB = OB, meaning that O is the same distance from each of the vertices of the triangle ABC.