Lets solve the Exercise 3.2 from Chapter 3 Understanding Quadrilaterals. Here you need to remember below concepts while solving the problem.
Sum of the Measures of the Exterior Angles of a Polygon
- Definition: Exterior angles are formed by extending one side of the polygon at each vertex.
- Sum of Exterior Angles: Always 360 degrees.
- Independent of Sides: The sum is 360 degrees regardless of the number of sides.
- Individual Exterior Angle (Regular Polygon):
- Formula: 360 degrees / number of sides
- n = number of sides
- Relationship to Interior Angles: Exterior angle + Interior angle = 180 degrees.
- Applications: Architecture, navigation, etc.
Things to Remember While Solving Questions
- Identify and label all exterior angles correctly.
- For regular polygons, use the formula for individual exterior angles.
- Check calculations to make sure the sum of exterior angles equals 360 degrees.
- Understand the relationship between interior and exterior angles.
- Review the properties of different polygons (triangle, quadrilateral, pentagon, etc.).
- Practice problems from the other textbook to clear concepts. We have very less questions in the NCERT book.
NCERT Solutions for Class 8 Maths Exercise 3.2 Chapter 3 Understanding Quadrilaterals
1. Find x in the following figures.
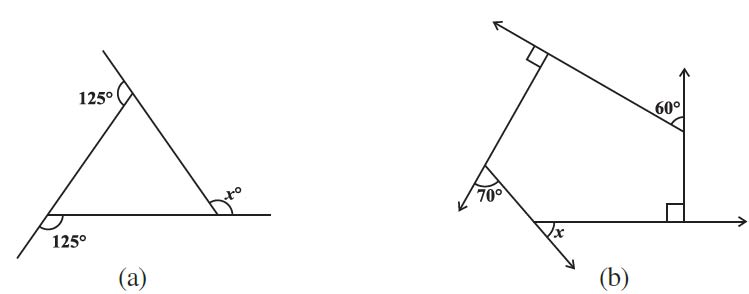
For figure (a), considering the exterior angles of the polygon, we know the sum of the exterior angles of any polygon is 360°.
Given that we have two exterior angles of 125° each, we can find x (also an exterior angle) as follows:
x + 125° + 125° = 360°
x = 360° – 125° – 125°
= 360° – 250°
= 110°
For Figure (b), we know that the sum of the exterior angles of a polygon is 180°. Let’s try to solve the problem –
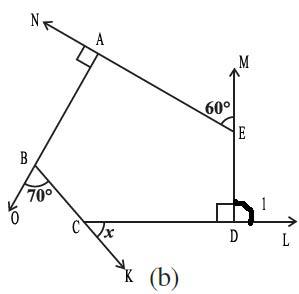
From the figure ABCDE, we know that –
∠EDC + ∠EDL = 180° (given ∠EDC = 90° and CL is a straight line)
90° + ∠EDL = 180°
∠EDL = 180° – 90°
We know that the sum of the exterior angles of a polygon is 360°. We now know all the exterior angles other than x –
x + 90° + 60° + 90° + 70° = 360°
x + 310° = 360°
x = 360° – 310°
x = 50°
Angle x = 50°
2. Find the measure of each exterior angle of a regular polygon of
(i) A regular polygon of 9 sides (nonagon):
Since the sum of the exterior angles of any polygon is 360°, the measure of each exterior angle of a regular nonagon is:
360° ÷ 9 = 40°
(ii) A regular polygon of 15 sides (pentadecagon):
Similarly, for a regular polygon of 15 sides:
360° ÷ 15 = 24°
3. How many sides does a regular polygon have if the measure of an exterior angle is 24°?
To find the number of sides (n) of a regular polygon with each exterior angle measuring 24°:
We know that the sum of all the exterior angles of a polygon is 360° –
360° ÷ 24° = n (where n is the number of exterior angles)
n = 15 sides
4. How many sides does a regular polygon have if each of its interior angles is 165°?
A polygon’s interior and exterior angles are supplementary (add up to 180°).
If each interior angle is 165°, then each exterior angle is:
180° – 165° = 15°
To find the number of sides (n) with each exterior angle measuring 15°:
360° ÷ 15° = n
n = 24 sides
5. (a) Is it possible to have a regular polygon with the measure of each exterior angle as 22°?
For a regular polygon, the measure of each exterior angle must be a divisor of 360°.
360° ÷ 22° is not a whole number
It is not possible to have a regular polygon with an exterior angle of 22°.
(b) Can it be an interior angle of a regular polygon? Why?
The interior angle (I) and the exterior angle (E) are supplementary. If the exterior angle is 22°, then the interior angle would be:
I = 180° – E
I = 180° – 22°
I = 158°
This is not a valid measure for an interior angle, as 158 is not a divisor of 360°
6. (a) What is the minimum interior angle possible for a regular polygon? Why?
A regular polygon is both equiangular and equilateral. It could be said that all sides and angles are equal.
An equilateral triangle is a regular polygon of equal 3 sides, and the minimum interior angle possible is 60°.
(b) What is the maximum exterior angle possible for a regular polygon?
The inner angle for an equilateral triangle is 60°.
The maximum exterior possible for a regular polygon will be –
Exterior angle = 180° – 60°
Exterior angle = 120°