We are towards the end of chapter 5 of the NCERT book for EXERCISE 5.3 in Squares and Square Roots. In Exercise 5.1, we learned about the properties of square numbers. Here, we are going to solve questions on –
- Pythagoras theorem
- Finding square roots
- Finding square root through repeated subtraction
- Finding square root through prime factorisation
Before we start solving the questions, let’s look at some of the basics you will require while solving the questions.
Exercise 5.3 Notes: Squares and Square Roots
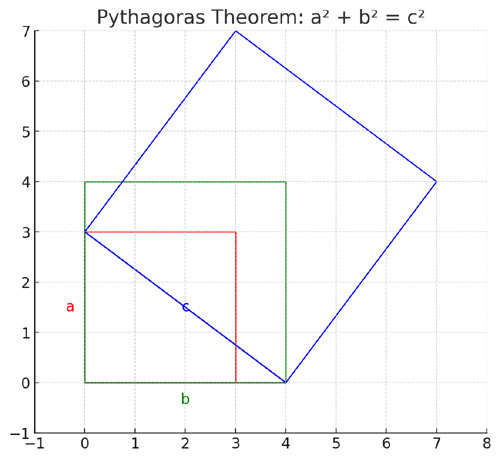
Pythagoras Theorem
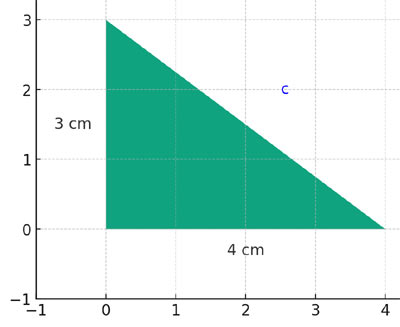
Example: For a right-angled triangle with sides 3 cm and 4 cm, find the hypotenuse (c):
c² = 3² + 4²
c² = 9 + 16
c² = 25
Hence, c = √25 or 5 cm.
Finding Square Roots
Example: For the square root of 16:
√25 = ?
Since 5 x 5 = 25, √25 = 5.
Finding Square Roots through Repeated Subtraction
Example: Square root of 16:
16 - 1 = 15
15 - 3 = 12
12 - 5 = 7
7 - 7 = 0
Four steps indicate the square root is 4.
Explanation of the above method:
This method works well for the perfect squares (like 16, 25, 36, etc.). Let’s break down the steps for finding the square root of 16:
Start with the number (in our case, 16).
Subtract consecutive odd numbers from this number, starting with 1, then 3, then 5, and so on, until you reach 0.
Count how many times you subtracted. This count will give you the square root of the original number.
Here’s why it works:
Square numbers are the sum of the first ‘n’ odd numbers. For example, 1+3+5+7 = 16.
When you subtract these odd numbers consecutively from a square number (like 16), you’re essentially reversing this summation process.
The number of odd numbers you subtract to get to zero is the same as the number of terms added to get the square number. This number is the square root.
In the case of 16:
16 – 1 = 15 (First subtraction)
15 – 3 = 12 (Second subtraction)
12 – 5 = 7 (Third subtraction)
7 – 7 = 0 (Fourth subtraction)
Since it took four steps (subtractions) to reach 0, the square root of 16 is 4.
Finding Square Roots through Prime Factorization
Example: Square root of 36:
Prime factors of 36: 2 x 2 x 3 x 3
Pairs: (2 x 2), (3 x 3)
Multiply one number from each pair: 2 x 3 = 6
So, the square root of 36 is 6.
Class 8 Maths for Chapter 5 Exercise 5.3 Squares and Square Roots – NCERT Book Solutions
1. What could be the possible ‘one’s’ digits of the square root of each of the following numbers?
(i) 9801 (ii) 99856 (iii) 998001 (iv) 657666025
Solution:
To figure out what the last digit of the square root might be, we look at the last digit of the original number. Then, we think about which numbers, when multiplied by themselves (squared), give us that same last digit.
For example, if a number ends in 1, we know that only two numbers, 1 and 9, when squared, will end in 1 (because 1 × 1 = 1 and 9 × 9 = 81, which ends in 1). So, the square root could end in either 1 or 9. We do this for each number to find out the possible last digits of their square roots.
Digits whose squares end in a specific digit:
0: 0² = 0
1: 1² = 1, 9² = 81
2: No digit squared ends in 2.
3: No digit squared ends in 3.
4: 2² = 4, 8² = 64
5: 5² = 25
6: 4² = 16, 6² = 36
7: No digit squared ends in 7.
8: No digit squared ends in 8.
9: 3² = 9, 7² = 49
(i) 9801
For 9801, one’s digit is 1
1: 1² = 1, 9² = 81
Square of 1 or 9 gives out 1 in one’s digit
Therefore, possible one’s digit of square root is 1 or 9
(ii) 99856
For 99856, one’s digit is 6
6: 4² = 16, 6² = 36
Square of 4 or 6 gives out 6 in one’s digit
Therefore, possible one’s digit of square root is 4 or 6
(iii) 998001
For 998001, one’s digit is 1
1: 1² = 1, 9² = 81
Square of 1 or 9 gives out 1 in one’s digit
Therefore, possible one’s digit of square root is 1 or 9
(iv) 657666025
For 657666025, one’s digit is 5
5: 5² = 25
Square of 5 or 5 gives out 5 in one’s digit (since 5² = 25)
Therefore, possible one’s digit of square root is 5
2. Without doing any calculation, find the numbers which are surely not perfect squares.
(i) 153 (ii) 257 (iii) 408 (iv) 441
Solution:
Without calculation, we can determine a number is not a perfect square if it ends in 2, 3, 7, or 8 because no square number ends in those digits:
(i) 153 is not a perfect square as it ends in 3.
(ii) 257 is not a perfect square as it ends in 7.
(iii) 408 is not a perfect square as it ends in 8.
(iv) 441 could be a perfect square as it ends in 1, and 1 is the square root of 1.
3. Find the square roots of 100 and 169 by the method of repeated subtraction.
100
100 – 1 = 99 (1st subtraction)
99 – 3 = 96 (2nd subtraction)
96 – 5 = 91 (3rd subtraction)
91 – 7 = 84 (4th subtraction)
84 – 9 = 75 (5th subtraction)
75 – 11 = 64 (6th subtraction)
64 – 13 = 51 (7th subtraction)
51 – 15 = 36 (8th subtraction)
36 – 17 = 19 (9th subtraction)
19 – 19 = 0 (10th subtraction)
From above we can see that the given number got reduced to 0 after subtracting from 1st 10 odd numbers
100 is a perfect square
√100 = 10
Therefore, the square root of 100 is 10.
169
169 – 1 = 168 (1st subtraction)
168 – 3 = 165 (2nd subtraction)
165 – 5 = 160 (3rd subtraction)
160 – 7 = 153 (4th subtraction)
153 – 9 = 144 (5th subtraction)
144 – 11 = 133 (6th subtraction)
133 – 13 = 120 (7th subtraction)
120 – 15 = 105 (8th subtraction)
105 – 17 = 88 (9th subtraction)
88 – 19 = 69 (10th subtraction)
69 – 21 = 48 (11th subtraction)
48 – 23 = 25 (12th subtraction)
25 – 25 = 0 (13th subtraction)
From above we can see that the given number got reduced to 0 after subtracting the first 13 odd numbers
169 is a perfect square
√169 = 13
Therefore, the square root of 169 is 13.
4. Find the square roots of the following numbers by the Prime Factorisation Method.
(i) 729 (ii) 400 (iii) 1764 (iv) 4096 (v) 7744 (vi) 9604 (vii) 5929 (viii) 9216 (ix) 529 (x) 8100
Solution:
For each number, factor it into primes and pair them to find the square root:
(i) 729
Using Prime Factorisation Method:
729 = 3 × 3 × 3 × 3 × 3 × 3
729 = (3 × 3 × 3)²
√729 = 3 × 3 × 3
So, the square root is 3 × 3 × 3 = 27
(ii) 400
Using Prime Factorisation Method:
400 = 2 × 2 × 2 × 2 × 5 × 5
400 = (2 × 2 × 5)²
√400 = 2 × 2 × 5
So, the square root is 2 × 2 × 5 = 20
(iii) 1764
Using Prime Factorisation Method:
1764 = 2 × 2 × 3 × 3 × 7 × 7
1764 = (2 × 3 × 7)²
√1764 = 2 × 3 × 7
So, the square root is 2 × 3 × 7 = 42
(iv) 4096
Using Prime Factorisation Method:
4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
4096 = (2 × 2 × 2 × 2 × 2 × 2)²
√4096 = 2 × 2 × 2 × 2 × 2 × 2
So, the square root is 2 × 2 × 2 × 2 × 2 × 2 = 64
(v) 7744
Using Prime Factorisation Method:
7744 = 2 × 2 × 2 × 2 × 2 × 2 × 7 × 7 (six 2’s and two 7’s)
7744 = (2 × 2 × 2 × 7)²
√7744 = 2 × 2 × 2 × 7
So, the square root is 2 × 2 × 2 × 7 = 88
(vi) 9604
Using Prime Factorisation Method:
9604 = 2 × 2 × 3 × 3 × 7 × 7 × 7 × 7
9604 = (2 × 3 × 7 × 7)²
√9604 = 2 × 3 × 7 × 7
So, the square root is 2 × 3 × 7 × 7 = 98
(vii) 5929
Using Prime Factorisation Method:
5929 = 7 × 7 × 7 × 7 × 7 × 7
5929 = (7 × 7 × 7)²
√5929 = 7 × 7 × 7
So, the square root is 7 × 7 × 7 = 77
(viii) 9216
Using Prime Factorisation Method:
9216 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
9216 = (2 × 2 × 2 × 2 × 3 × 3)²
√9216 = 2 × 2 × 2 × 2 × 3 × 3
So, the square root is 2 × 2 × 2 × 2 × 3 × 3 = 96
(ix) 529
Using Prime Factorisation Method:
529 = 23 × 23
529 = (23)²
√529 = 23
So, the square root is 23 = 23
(x) 8100
Using Prime Factorisation Method:
8100 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5
8100 = (2 × 3 × 3 × 5)²
√8100 = 2 × 3 × 3 × 5
So, the square root is 2 × 3 × 3 × 5 = 90
5. For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
(i) 252 (ii) 180 (iii) 1008 (iv) 2028 (v) 1458 (vi) 768
Solution:
For each number, we find the smallest whole number to multiply to get a perfect square and then determine the square root.
(i) 252
Using Prime Factorisation Method:
252 = 2 × 2 × 3 × 3 × 7
To make it a perfect square, One more 7 is required.
We need to multiply the given number by 7
Therefore, 252 × 7 = 1764 is perfect square
1764 = 2 × 2 × 3 × 3 × 7 × 7
= (2 × 3 × 7)²
√1764 = 2 × 3 × 7 = 42
The perfect square is 1764, and the square root is 42.
(ii) 180
Using Prime Factorisation Method:
180 = 2 × 2 × 3 × 3 × 5
To make it a perfect square, One more 5 is required.
We need to multiply the given number by 5
Therefore, 180 × 5 = 900 is a perfect square
900 = 2 × 2 × 3 × 3 × 5 × 5
= (2 × 3 × 5)²
√900 = 2 × 3 × 5 = 30
The perfect square is 900, and the square root is 30.
(iii) 1008
Using Prime Factorisation Method:
1008 = 2 × 2 × 2 × 2 × 3 × 3 × 7
To make it a perfect square, One more 7 is required.
We need to multiply the given number by 7
Therefore, 1008 × 7 = 7056 is a perfect square
7056 = 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
= (2 × 2 × 3 × 7)²
√7056 = 2 × 2 × 3 × 7 = 84
The perfect square is 7056, and the square root is 84.
(iv) 2028
Using Prime Factorisation Method:
2028 = 2 × 2 × 3 × 13 × 13
To make it a perfect square, One more 3 is required.
We need to multiply the given number by 3
Therefore, 2028 × 3 = 6084 is a perfect square
6084 = 2 × 2 × 3 × 3 × 13 × 13
= (2 × 3 × 13)²
√6084 = 2 × 3 × 13 = 78
The perfect square is 6084, and the square root is 78.
(v) 1458
Using Prime Factorisation Method:
1458 = 2 × 3 × 3 × 3 × 3 × 3 × 3
To make it a perfect square, One more 2 is required.
We need to multiply the given number by 2
Therefore, 1458 × 2 = 2916 is a perfect square
2916 = 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
= (2 × 3 × 3 × 3 × 3)²
√2916 = 2 × 3 × 3 × 3 × 3 = 54
The perfect square is 2916, and the square root is 54.
(vi) 768
Using Prime Factorisation Method:
768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
To make it a perfect square, One more 3 is required.
We need to multiply the given number by 3
Therefore, 768 × 3 = 2304 is a perfect square
2304 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
= (2 × 2 × 2 × 2 × 3)²
√2304 = 2 × 2 × 2 × 2 × 3 = 48
The perfect square is 2304, and the square root is 48.
6. For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also find the square root of the square number so obtained.
(i) 252 (ii) 2925 (iii) 396 (iv) 2645 (v) 2800 (vi) 1620
Solution:
For each number, we find the smallest whole number to divide to get a perfect square and then determine the square root.
(i) 252
Using Prime Factorisation Method:
252 = 2 × 2 × 3 × 3 × 7.
The prime factor 7 has no pair. In order to get the perfect square, the given number should be divided by 7
Therefore, 252/7 = 36 is a perfect square
Using Prime Factorisation Method:
36 = 2 × 2 × 3 × 3 = (2 × 3)²
√36 = 6
The perfect square is 36, and the square root is 6
(ii) 2925
Using Prime Factorisation Method:
2925 = 3 × 3 × 5 × 5 × 13
The prime factor 13 has no pair. In order to get the perfect square, the given number should be divided by 13
Therefore, 2925 / 13 = 225 is a perfect square
Using Prime Factorisation Method:
225 = 3 × 3 × 5 × 5 = (3 × 5)²
√225 = 15
The perfect square is 225, and the square root is 15.
(iii) 396
Using Prime Factorisation Method:
396 = 2 × 2 × 3 × 3 × 11
The prime factor 11 has no pair. In order to get the perfect square, the given number should be divided by 11
Therefore, 396 / 11 = 36 is a perfect square
Using Prime Factorisation Method:
36 = 2 × 2 × 3 × 3 = (2 × 3)²
√36 = 6
The perfect square is 36, and the square root is 6.
(iv) 2645
Using Prime Factorisation Method:
2645 = 5 × 23 × 23
The prime factor 5 has no pair. In order to get the perfect square, the given number should be divided by 5
Therefore, 2645 / 5 = 529 is a perfect square
Using Prime Factorisation Method:
529 = 23 × 23 = (23)²
√529 = 23
The perfect square is 529, and the square root is 23.
(v) 2800
Using Prime Factorisation Method:
2800 = 2 × 2 × 2 × 2 × 5 × 5 × 7
The prime factor 7 has no pair. In order to get the perfect square, the given number should be divided by 7
Therefore, 2800 / 7 = 400 is a perfect square
Using Prime Factorisation Method:
400 = 2 × 2 × 2 × 2 × 5 × 5 = (2 × 2 × 5)²
√400 = 20
The perfect square is 400, and the square root is 20.
(vi) 1620
Using Prime Factorisation Method:
1620 = 2 × 2 × 3 × 3 × 3 × 3 × 5
The prime factor 5 has no pair. In order to get the perfect square, the given number should be divided by 5
Therefore, 1620 / 5 = 324 is a perfect square
Using Prime Factorisation Method:
324 = 2 × 2 × 3 × 3 × 3 × 3 = (2 × 3 × 3)²
√324 = 18
The perfect square is 324, and the square root is 18.
7. The students of Class VIII of a school donated ? 2401 in all, for Prime Minister’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Solution:
Since each student donated as many rupees as the number of students in the class, the total donation (? 2401) must be a perfect square. To find the number of students, we calculate the square root of 2401.
The prime factorization of 2401 is 7 × 7 × 7 × 7.
The square root of 2401 is 7 × 7 = 49.
Therefore, there are 49 students in the class.
8. 2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Solution:
We need to find a square number that equals 2025, where the square root of the number will give us both the number of rows and the number of plants per row.
The prime factorization of 2025 is 3 × 3 × 3 × 3 × 5 × 5.
The square root of 2025 is 3 × 3 × 5 = 45.
Therefore, the garden has 45 rows, with 45 plants in each row.
9. Find the smallest square number that is divisible by each of the numbers 4, 9 and 10.
Solution:
The least common multiple (LCM) of 4 (2 × 2), 9 (3 × 3), and 10 (2 × 5) gives us the smallest number divisible by all, but we need to ensure it’s a perfect square.
The LCM is 2 × 2 × 3 × 3 × 5.
To make it a perfect square, we need another 5, so the number is 2 × 2 × 3 × 3 × 5 × 5 = 900.
The smallest square number divisible by 4, 9, and 10 is 900.
10. Find the smallest square number that is divisible by each of the numbers 8, 15 and 20.
Solution:
We start with the LCM of 8 (2 × 2 × 2), 15 (3 × 5), and 20 (2 × 2 × 5), which includes the highest powers of primes from each number.
The LCM is 2 × 2 × 2 × 3 × 5.
To make this a perfect square, we multiply by another 2 (to pair the 2s) and another 3 × 5 (to pair the 3 and 5).
The smallest square number is 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 = 3600.
Therefore, the smallest square number divisible by 8, 15, and 20 is 3600.
Practice Worksheet with Challenging Questions For Class 8 Maths for Ex. 5.3
Questions
- Find the least number that must be added to 1500 to make it a perfect square.
- Find the least number subtracted from 2000 to make it a perfect square.
- Determine the square root of 88209 by repeated subtraction.
- What is the smallest square number that is divisible by each of the numbers 24, 36, and 45?
- How many numbers lie between squares of 25 and 26?
- If the 7-digit square number 25X6489 ends with a square number, find X.
- Find the value of √(0.0081) + √(0.000169) without using a calculator.
- Without calculating the square roots, arrange the numbers in increasing order: 0.04, 1/16, 0.0009, 1/81.
- By prime factorization, find the square roots of 7056.
- Find the square of 53 using the identity (a+b)² = a² + 2ab + b².
- If the area of a square is 1225 sq. cm, find the length of its diagonal.
- The product of two numbers is 6400, and their quotient is 4. Find the numbers.
- Find the least number that must be multiplied by 1800 to make it a perfect cube.
- If the square of a number is 1089, what is the value of the square of the number increased by 4?
- Determine the smallest number by which 360 must be divided to become a perfect square.
Answers with Hints
- The least number to be added to 1500 to make it a perfect square is 25. Adding this, we get 1525, which is 39².
- The least number that must be subtracted from 2000 to make it a perfect square is 1. Subtracting this, we get 1999, which is 44².
- The square root of 88209 by the method of repeated subtraction is 297.
- The smallest square number divisible by 24, 36, and 45 is 3600.
- There are 50 numbers between the squares of 25 and 26.
- If the square number 25X6489 ends with a square number, then X is 6.
- The value of √(0.0081) + √(0.000169) is 0.09 + 0.013 = 0.103.
- Increasing order: 0.0009, 1/81, 1/16, 0.04.
- The square root of 7056 by prime factorization is 84.
- The square of 53 is 2809.
- The length of the diagonal of a square with an area of 1225 sq. cm is 49 cm.
- The two numbers are 80 and 20.
- The least number that must be multiplied by 1800 to make it a perfect cube is 5.
- If the square of a number is 1089, the square of the number increased by 4 is 11881.
- The smallest number by which 360 must be divided to become a perfect square is 10.