In the exercise 9.1 of Mensuration for class 8, we are going to solve questions about Area of a Polygon. Lets have a look at some of the basics you would require to solve the questions.
Area of a Polygon
Area of a Trapezium
The area of a trapezium can be calculated using the formula:
Area = 1/2 × (Sum of the lengths of the parallel sides) × Height
For example, if a trapezium has parallel sides of lengths 8 cm and 5 cm, and the height (the perpendicular distance between the parallel sides) is 4 cm, then its area is:
Area = 1/2 × (8 cm + 5 cm) × 4 cm = 1/2 × 13 cm × 4 cm = 26 cm².
Area of a Rhombus
The area of a rhombus is given by the formula:
Area = 1/2 × (Product of the diagonals)
For instance, if the diagonals of a rhombus measure 10 cm and 6 cm, the area is:
Area = 1/2 × 10 cm × 6 cm = 30 cm².
Area of a Regular Hexagon
A regular hexagon can be divided into six equilateral triangles. The area of a regular hexagon is:
Area = (3√3/2) × (Side length)²
As an example, if the side of a regular hexagon is 2 cm, then its area is:
Area = (3√3/2) × (2 cm)² = (3√3/2) × 4 cm² ≈ 10.392 cm².
[joli-toc]
NCERT Solutions Class 8 Maths for Chapter 9 Ex. 9.1 Mensuration
1. The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and the perpendicular distance between them is 0.8 m.
Solution
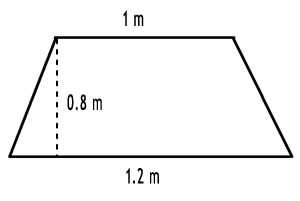
The area (A) of a trapezium can be calculated using the formula: 1/2 × (a + b) × h
where: a and b are the lengths of the parallel sides,
h is the perpendicular distance (height) between the parallel sides.
The area of a trapezium is given by the formula: A = 0.5 × (sum of the lengths of the parallel sides) × (perpendicular distance between the parallel sides).
Here, the length of the first parallel side (a) = 1 m.
The length of the second parallel side (b) = 1.2 m.
The perpendicular distance (height, h) = 0.8 m.
Substituting the values, we get A = 0.5 × (1 m + 1.2 m) × 0.8 m = 0.5 × 2.2 m × 0.8 m = 0.88 m².
Therefore, the area of the top surface of the table is 0.88 m².
2. The area of a trapezium is 34 cm² and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.
Solution
Let the length of the other parallel side be x cm.
The area of a trapezium is given by the formula: A = 0.5 × (sum of the lengths of the parallel sides) × height.
Substituting the given values, we have 34 cm² = 0.5 × (10 cm + x cm) × 4 cm.
Simplifying, 34 cm² = (10 cm + x cm) × 2 cm.
Dividing both sides by 2 cm, we get 17 cm = 10 cm + x.
Therefore, the length of the other parallel side x = 17 cm – 10 cm = 7 cm.
3. Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.
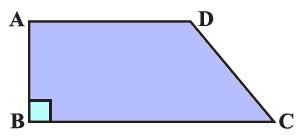
Solution
The area (A) of a trapezium can be calculated using the formula:
A = 1/2 × (a + b) × h
Where
– a and b are the lengths of the parallel sides AD and BC,
– h is the height (AB) of the trapezium.
We are given:
BC = 48 m (one of the parallel sides),
AD = 40 m (the other parallel side),
The length of the fence, which is the perimeter of the field, is 120 m.
Since AB is perpendicular to both AD and BC, AB + CD + AD + BC = Perimeter of the field.
We need to find the length AB to compute the area. We can find AB using the perimeter –
Given the lengths of sides BC = 48 m, CD = 17 m, and AD = 40 m, and the total fence length (perimeter) is 120 m.
We first find the length of side AB, which is the height of the trapezium, using the perimeter:
AB = Perimeter – AD – BC – CD = 120 m – 40 m – 48 m – 17 m = 15 m.
The area of the trapezium is then calculated by the formula:
A = 0.5 × (AD + BC) × AB = 0.5 × (40 m + 48 m) × 15 m = 660 m².
Therefore, the area of the trapezium-shaped field ABCD is 660 m².
4. The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
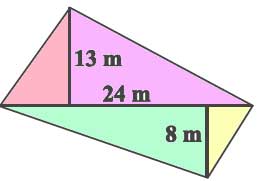
Solution
The area (A) of a triangle with a base (b) and a height (h) is given by:
A = 1/2 × b × h
For this quadrilateral, the diagonal acts as the base for both triangles, and the perpendiculars are the heights.
Given:
The length of the diagonal (base for both triangles) is 24 m.
The perpendicular from one vertex (height of one triangle) is 8 m.
The perpendicular from the other vertex (height of the second triangle) is 13 m.
Let’s calculate the area of each triangle and then sum them to find the total area of the field:
The area of the field is the sum of the areas of two triangles created by the diagonal.
Area of the first triangle with height 8 m: A₁ = 1/2 × 24 m × 8 m = 96 m².
Area of the second triangle with height 13 m: A₂ = 1/2 × 24 m × 13 m = 156 m².
Total area of the field: A = A₁ + A₂
Total area of the field = 96 m² + 156 m² = 252 m².
Therefore, the area of the quadrilateral-shaped field is 252 m².
5. The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Solution
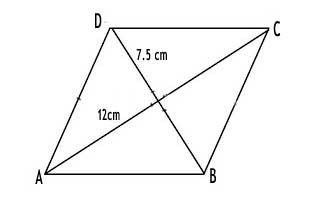
The area of a rhombus is given by the formula: A = 0.5 × (product of the diagonals).
Therefore, A = 0.5 × 7.5 cm × 12 cm = 45 cm².
So, the area of the rhombus is 45 cm².
6. Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Solution
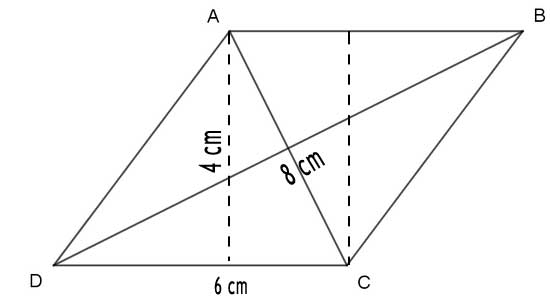
The area of a rhombus is also equal to the product of its base (side) and height (altitude).
A = side × altitude = 5 cm × 4.8 cm = 24 cm².
For the diagonals, the area of a rhombus is also given by the formula: A = 0.5 × (product of the diagonals).
Let the length of the other diagonal be d cm. Then,
24 cm² = 0.5 × 8 cm × d cm.
Simplifying, d = (24 cm² / 4 cm) = 6 cm.
Therefore, the length of the other diagonal is 6 cm.
7. The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m² is ₹ 4.
Solution
The area of one tile (rhombus) is A = 0.5 × (product of the diagonals) = 0.5 × 45 cm × 30 cm = 675 cm².
To convert to square meters, divide by 10,000 (since 1 m² = 10,000 cm²).
Area of one tile in square meters = 675 cm² / 10,000 = 0.0675 m².
Total area for 3000 tiles = 3000 × 0.0675 m² = 202.5 m².
Total cost for polishing = Total area × Cost per m² = 202.5 m² × ₹ 4 = ₹ 810.
So, the total cost of polishing the floor is ₹ 810.
8. Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
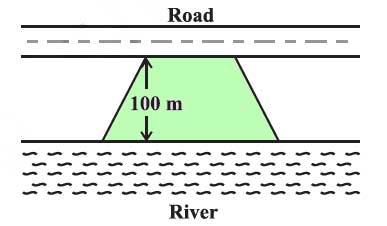
Solution:
Mohan is interested in purchasing a trapezium-shaped field. The side along the river is parallel to and twice as long as the side along the road. Given the field’s area is 10,500 m2 and the perpendicular distance between the two parallel sides is 100 m, we need to calculate the length of the side along the river.
We use the area formula for a trapezium:
Area = (1/2) * (sum of the lengths of the parallel sides) * height
Let the length of the side along the road be ‘x’ meters. Then the length of the side along the river is ‘2x’ meters.
Substituting the given values into the area formula we get:
10,500 m² = (1/2) * (x + 2x) * 100 m
Simplifying, we find:
10,500 m² = 150x m²
Solving for ‘x’ gives us:
x = 70 meters.
Therefore, the length of the side along the river, which is twice the length of the side along the road, is:
2x = 2 * 70 = 140 meters.
So, the length of the side along the river is 140 meters.
10. There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways. Find the area of this park using both ways. Can you suggest some other way of finding its area?
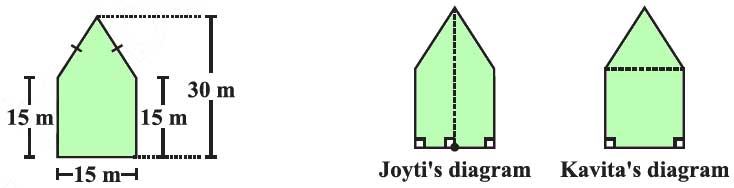
Solution:
To find the area of the pentagonal park, Jyoti and Kavita divided it in two different ways.
Jyoti’s Method:
Jyoti divides the park into a rectangle and two triangles.
– The area of the rectangle = length × width = 15 m × 15 m = 225 m².
– The area of the two triangles = 2 × (1/2 × base × height) = 2 × (1/2 × 15 m × 15 m) = 225 m².
– Total area using Jyoti’s method = 225 m² + 225 m² = 450 m².
Kavita’s Method:
Kavita divides the park into a triangle and a trapezium.
– The area of the triangle = 1/2 × base × height = 1/2 × 15 m × 15 m = 112.5 m².
– The area of the trapezium = 1/2 × (sum of parallel sides) × height = 1/2 × (15 m + 30 m) × 15 m = 337.5 m².
– Total area using Kavita’s method = 112.5 m² + 337.5 m² = 450 m².
Alternative Method:
Another method to calculate the area could be to divide the park into three triangles and calculate the area of each triangle, then sum them up. This would require knowing all the necessary dimensions.
11. Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.
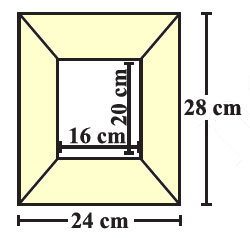
Solution:
The picture frame has outer dimensions of 24 cm by 28 cm and inner dimensions of 16 cm by 20 cm. The frame’s sections are uniform in width.
First, we calculate the width of the frame sections:
– The width of the horizontal sections: (24 cm – 16 cm) / 2 = 4 cm.
– The width of the vertical sections: (28 cm – 20 cm) / 2 = 4 cm.
Next, we find the area of each section:
– Area of one horizontal section = 24 cm × 4 cm = 96 cm².
– Area of one vertical section = 28 cm × 4 cm = 112 cm².
Therefore, each horizontal section of the frame has an area of 96 cm², and each vertical section has an area of 112 cm².
Extra Challenging MCQ Questions for Exercise 9.1 Mensuration
1. The area of a trapezium is 150 cm², and the lengths of its parallel sides are 10 cm and 20 cm. What is the height of the trapezium?
Formula: Area of trapezium = 1/2 x (Sum of parallel sides) x Height
a) 5 cm
b) 10 cm
c) 15 cm
d) 20 cm
Answer:
b) 10 cm
2. A rhombus has diagonals measuring 16 cm and 12 cm. What is its area?
Formula: Area of rhombus = 1/2 x (Product of diagonals)
a) 48 cm²
b) 96 cm²
c) 192 cm²
d) 24 cm²
Answer:
b) 96 cm²
3. The side length of a regular hexagon is 6 cm. What is its area? (Use √3 ≈ 1.732)
Formula: Area of regular hexagon = (3√3/2) x (Side length)²
a) 54 cm²
b) 93.53 cm²
c) 108 cm²
d) 64.78 cm²
Answer:
b) 93.53 cm²
4. If the area of a rhombus is 120 cm² and one of its diagonals is 10 cm, what is the length of the other diagonal?
Formula: Area of rhombus = 1/2 x (Product of diagonals)
a) 12 cm
b) 24 cm
c) 20 cm
d) 15 cm
Answer:
c) 24 cm
5. A trapezium has an area of 84 m², with one parallel side measuring 8 m and the height being 7 m. What is the length of the other parallel side?
Formula: Area of trapezium = 1/2 x (Sum of parallel sides) x Height
a) 16 m
b) 14 m
c) 12 m
d) 10 m
Answer:
a) 16 m
6. The diagonals of a rhombus are in the ratio 3:4, and its area is 96 cm². What are the lengths of the diagonals?
Formula: Area of rhombus = 1/2 x (Product of diagonals)
a) 6 cm and 8 cm
b) 12 cm and 16 cm
c) 9 cm and 12 cm
d) 15 cm and 20 cm
Answer:
b) 12 cm and 16 cm
7. A regular hexagon has a perimeter of 72 cm. What is its area? (Use √3 ≈ 1.732)
Formula: Area of regular hexagon = (3√3/2) x (Side length)²; Side length = Perimeter ÷ 6
a) 216 cm²
b) 374.76 cm²
c) 432 cm²
d) 259.81 cm²
Answer:
b) 374.76 cm²
8. The area of a trapezium is 60 cm², and its height is 5 cm. If one of the parallel sides is twice the length of the other, what are the lengths of the parallel sides?
Formula: Area of trapezium = 1/2 x (Sum of parallel sides) x Height
a) 6 cm and 12 cm
b) 8 cm and 16 cm
c) 10 cm and 20 cm
d) 4 cm and 8 cm
Answer:
a) 6 cm and 12 cm
9. A rhombus has sides of length 10 cm and one of its diagonals is 16 cm. What is its area?
Formula: Area of rhombus = 1/2 x (Product of diagonals); Use Pythagoras theorem to find the second diagonal.
a) 48 cm²
b) 96 cm²
c) 80 cm²
d) 60 cm²
Answer:
c) 80 cm²
10. The side length of a regular hexagon is increased by 50%. By what percentage does its area increase?
Formula: Area of regular hexagon = (Side length)²; New Area = 1.5² x Old Area; Percentage increase = [(New Area – Old Area)/Old Area] x 100
a) 50%
b) 100%
c) 125%
d) 150%
Answer:
c) 125%
Practice Worksheet with Challenging Questions For Class 8 Maths for Ex. 9.1 Mensuration
Questions
- Calculate the area of a trapezium with bases of 12 cm and 19 cm and a height of 15 cm.
- A rhombus has a side length of 10 cm and one diagonal of 16 cm. Find the area.
- Find the area of a regular hexagon with a side length of 14 cm.
- Calculate the area of a parallelogram with a base of 24 cm and a corresponding height of 10 cm.
- If the area of a regular pentagon is 540 cm², find the length of its side, given the apothem length is 12 cm.
- Determine the length of the diagonal of a square with an area of 625 cm².
- Find the area of an equilateral triangle with a perimeter of 54 cm.
- A circle and a square have the same perimeter. If the circle’s radius is 14 cm, find the area of the square.
- Calculate the area of a circular sector with a radius of 7 cm and an angle of 120 degrees.
- Find the area of a rectangle whose diagonal is 25 cm and one side is 24 cm.
- The perimeter of an isosceles right triangle is 72 cm. Determine its area.
- Find the area of a kite with diagonals measuring 18 cm and 24 cm.
- A trapezium has an area of 360 cm² and a height of 12 cm. If one base is 20 cm, find the other base.
- Determine the circumference of a circle if its area is equal to the area of a rectangle with dimensions 28 cm by 22 cm.
- Find the side length of a square whose area is equal to the area of a triangle with a base of 48 cm and height of 32 cm.
Answers
- Area of a trapezium = 1/2 * (sum of parallel sides) * height.
- Area of a rhombus = 1/2 * (product of diagonals).
- Area of a regular hexagon = (3√3/2) * (side length)².
- Area of a parallelogram = base * height.
- Area of a regular pentagon = 1/2 * perimeter * apothem.
- Diagonal of a square = √(area) * √2.
- Area of an equilateral triangle = (√3/4) * (side length)²; use the perimeter to find the side length first.
- Perimeter of a square = circumference of a circle; then find the area of the square.
- Area of a circular sector = 1/2 * r² * θ (in radians).
- Area of a rectangle = base * height; use the Pythagorean theorem to find the missing side.
- Area of an isosceles right triangle = 1/2 * (leg length)²; use the perimeter to find the leg length.
- Area of a kite = 1/2 * (product of diagonals).
- Area of a trapezium = 1/2 * (sum of parallel sides) * height; use the given values to find the unknown base.
- Circumference of a circle = 2 * π * r; set the area of the circle equal to the area of the rectangle to find r.
- Area of a square = (side length)²; set this equal to the area of the triangle to solve for the side length.