NCERT Solutions for Class 8 Maths Exercise 6.1 Chapter 6 Cubes and Cube Roots
1. Which of the following numbers are not perfect cubes?
(i) 216 (ii) 128 (iii) 1000 (iv) 100 (v) 46656
(i) 216
Prime factors of 216 –
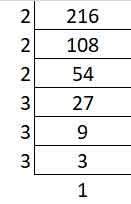
216 = 2 × 2 × 2 × 3 × 3 × 3
The prime factors of 2 and 3 occur in groups of three.
216 is a perfect cube.
(ii) 128
Prime factors of 128 –
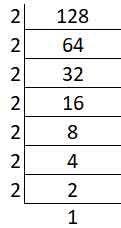
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
The prime factors of 2 do not form complete groups of three as there are 7 twos.
128 is not a perfect cube.
(iii) 1000
Prime factors of 1000 –
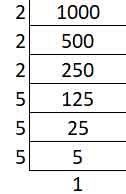
1000 = 2 × 2 × 2 × 5 × 5 × 5
The prime factors of 2 and 5 occur in groups of three.
1000 is a perfect cube.
(iv) 100
Prime factors of 100 –
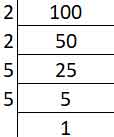
100 = 2 × 2 × 5 × 5
The prime factors of 2 and 5 do not form complete groups of three.
100 is not a perfect cube.
(v) 46656
Prime factors of 46656 –
46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
The prime factors of 2 and 3 occur in groups of six, which is a multiple of three.
46656 is a perfect cube.
2. Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.
(i) 243 (ii) 256 (iii) 72 (iv) 675 (v) 100
(i) 243
When we resolve 243 into its prime factors, we get –
243 = 3 x 3 x 3 x 3 x 3 = 3³ x 3²
The prime factors does not appear in group of three.
Given number 243 is not a perfect cube.
It needs one more 3 = 3³ x 3² x3
3³ x 3³ = 729
243 should be multiplied by 3 to get a perfect cube
Therefore, Smallest number = 3.
(ii) 256
Resolving 256 into its prime factors, we get –
256 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
Above, the prime factor 2, does not appear in group of three = 2³ x 2³ x 2²
256 is not a perfect cube.
In order to make it a perfect cube, we require one more 2 = 2³ x 2³ x 2² x 2
2³ x 2³ x 2³ = 512
Smallest number = 2.
(iii) 72
We try Resolving 72 into its prime factors, we get –
72 = 2 x 2 x 2 x 3 x 3
Above, the prime factor 2, is in group of three, but 3 is not in group of three = 2³ x 3²
72 is not a perfect cube
It needs one more one more 3 = 2³ x 3² x 3
2³ x 3³ = 216
Smallest number = 3
(iv) 675
Resolving 675 into its prime factors, we get –
675 = 3 x 3 x 3 x 5 x 5
The prime factor 3, is in group of three, but 5 is not in group of three = 2³ x 5²
We can say that 675 is not a perfect cube
It needs one more 5 for perfect cube = 3³ x 5² x 5
3³ x 5³ = 3375
Smallest number = 5.
(v) 100
Breaking down 100 into its prime factors, we get –
100 = 2 x 2 x 5 x 5 = 2² x 5²
The prime factor 2 and 5 both are not in group of three = 2² x 5²
100 is not a perfect cube.
We require one more 2 and one more 5 in order to make it a perfect root = 2² x 2 x 5² x 5
2³ x 5³ = 1000
Smallest number = 2 x 5 = 10.
3. Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.
(i) 81 (ii) 128 (iii) 135 (iv) 192 (v) 704
(i) 81
Breaking down 81 into its prime factors, we get –
81 = 3 x 3 x 3 x 3
The prime factor 3 is in group of 3 but there is an extra 4th factor 3 = 3³ x 3
81 is not a perfect cube
In order to make it a perfect root, we can remove extra 3 by division
divide by 3 = (3³ x 3)/3 = 3³
Smallest number = 3.
(ii) 128
We are breaking down 128 into its prime factors, we get –
128 = 2 x 2 x 2 x 2 x 2 x 2 x 2
The prime factor 2 is in group of three but there is an extra 2 = = 2³ x 2³ x 2
128 is not a perfect cube
We can make it a perfect root by removing extra 3 by division –
divide by 2 = (2³ x 2³ x 2)/2 = 2³ x 2³
Smallest number = 2.
(iii) 135
We are resolving 135 into its prime factors –
135 = 3 x 3 x 3 x 5
The prime factor 3 is in group of three but there is an extra 5 = 3³ x 5
From the above, we know that 135 is not a perfect root.
We can make it a perfect root by removing extra 5 by division –
Divide by 5 = (3³ x 5)/5 = 3³
Smallest number = 5.
(iv) 192
Resolving 192 into its prime factors –
192 = 2 x 2 x 2 x 2 x 2 x 2 x 3
The prime factor 2 is in group of three but there is an extra 3 = 2³ x 2³ x 3
192 is not a perfect cube
We make it a perfect root by removing extra 3 by division –
Divide by 3 = (2³ x 2³ x 3)/3 = 2³ x 2³
Smallest number = 3.
(v) 704
We resolving 704 into its prime factors –
704 = 2 x 2 x 2 x 2 x 2 x 2 x 11
Though factor 2 is in group of three, there is an lone 11 = 2³ x 2³ x 11
704 is not a perfect cube root
We are going to make it a perfect root by removing extra 11 by division –
Divide by 11 = (2³ x 2³ x 11)/11 = 2³ x 2³
Smallest number = 11.
4. Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
In the above, cuboid sides are given as 5cm, 2cm, and 5cm
Volume of one cuboid = l x b x h
= 5 cm x 2 cm x 5 cm = 50 cm³
To form a cube, the volume should be a perfect cube where dimension should be in a group of three
We find the prime factor of 50 = 2 x 5 x 5
To make it a perfect cube, we need to multiple 50 by 2 twos, and 1 five = 2 x 2 x 5
= 20
Additional Questions similar to 6.1 Chapter 6 Cubes and Cube Roots
1. Which of the following numbers are not perfect cubes?
(i) 343
343 = 7 x 7 x 7, so it is a perfect cube.
(ii) 250
250 = 2 x 5 x 5 x 5, not a perfect cube (uneven grouping for cube).
(iii) 3375
3375 = 3 x 3 x 3 x 5 x 5 x 5, so it is a perfect cube.
(iv) 800
800 = 2 x 2 x 2 x 2 x 2 x 5 x 5, not a perfect cube (uneven grouping for cube).
(v) 729
729 = 3 x 3 x 3 x 3 x 3 x 3, not a perfect cube (uneven grouping for cube).
2. Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.
(i) 500
500 = 2 x 2 x 5 x 5 x 5, needs one more 2.
Smallest number = 2.
(ii) 450
450 = 2 x 3 x 3 x 5 x 5
Needs two more 2 and one more 3 and 5 each = 2 x 2 x 2 x 3 x 3 x 3 x 5 x 5 x 5
Smallest number = 2 x 2 x 3 x 5 = 60.
(iii) 162
162 = 2 x 3 x 3 x 3 x 3, needs two more 2 and two more 3s.
Smallest number = 2 x 2 x 3 x 3 = 36.
(iv) 196
196 = 2 x 2 x 7 x 7, needs one more 2 and one more 7.
Smallest number = 2 x 7 = 14.
(v) 50
50 = 2 x 5 x 5, needs two more 2s and 1 more 5.
Smallest number = 2 x 2 x 5 = 20.
3. Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.
(i) 500
500 = 2 x 2 x 5 x 5 x 5
divide by 2 x 2 = 4.
Smallest number = 4.
(ii) 270
270 = 2 x 3 x 3 x 3 x 5
divide by 2, and 5.
Smallest number = 2 x 5 = 10
(iii) 1024
1024 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
divide by 2
Smallest number = 2