Cube roots deals with volumes and three-dimensional shapes. The cube root of a number is a value which when cubed, equals the original number. For example, the cube root of 27 is 3 because 3³ equals 27. This is written as ∛27 = 3.
For cube root of 64, the calculation is as follows: 4³ equals 64, so ∛64 = 4.
Cube roots are not always whole numbers; for instance, ∛2 is approximately 1.2599 since 1.2599³ is nearly equal to 2.
In geometry, cube roots help find an edge length of a cube from its volume. If a cube has a volume of 216 cubic units, its edge length is ∛216, which is 6 units.
Knowing cube roots is vital for solving various mathematical problems involving volume and three-dimensional geometry.
NCERT Solutions for Class 8 Maths Exercise 6.2 Chapter 6 Cubes and Cube Roots
1. Find the cube root of each of the following numbers by prime factorisation method.
(i) 64 (ii) 512 (iii) 10648 (iv) 27000 (v) 15625 (vi) 13824 (vii) 110592 (viii) 46656 (ix) 175616 (x) 91125
(i) Cube root of 64:
Solution:
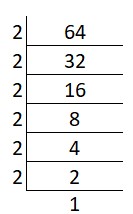
Prime factors of 64 = 2 x 2 x 2 x 2 x 2 x 2
Group the factors in triples: ∛(2 x 2 x 2 x 2 x 2 x 2)
∛(4 x 4 x 4)
Cube root = 4
(ii) Cube root of 512:
Solution:
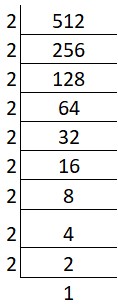
Prime factors of 512 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
Group the factors in triples: ∛(2 x 2 x 2) x (2 x 2 x 2) x (2 x 2 x 2)
Cube root = 2 x 2 x 2 = 8
(iii) Cube root of 10648:
Solution:
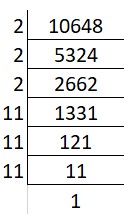
Prime factors of 10648 = 2 x 2 x 2 x 11 x 11 x 11
Group the factors in triples: ∛(2 x 2 x 2) x (11 x 11 x 11)
Cube root = 2 x 11 = 22
(iv) Cube root of 27000:
Solution:
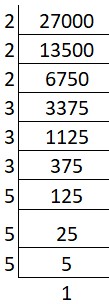
Prime factors of 27000 = 2 x 2 x 2 x 3 x 3 x 3 x 5 x 5 x 5
Group the factors in triples: ∛(2 x 2 x 2) x (3 x 3 x 3) x (5 x 5 x 5)
Cube root = 2 x 3 x 5 = 30
(v) Cube root of 15625:
Solution:
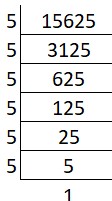
Prime factors of 15625 = 5 x 5 x 5 x 5 x 5 x 5
Group the factors in triples: ∛(5 x 5 x 5) x (5 x 5 x 5)
Cube root = 5 x 5 = 25
(vi) Cube root of 13824:
Solution:
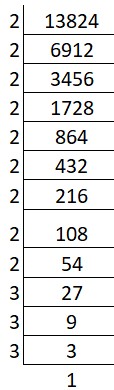
Prime factors of 13824 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3
Group the factors in triples: ∛(2 x 2 x 2) x (2 x 2 x 2) x (2 x 2 x 2) x (3 x 3 x 3)
Cube root = 2 x 2 x 2 x 3 = 24
(vii) Cube root of 110592:
Solution:
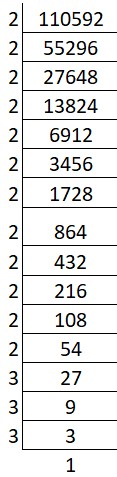
Prime factors of 110592 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3
Group the factors in triples: ∛(2 x 2 x 2) x (2 x 2 x 2) x (2 x 2 x 2) x (2 x 2 x 2) x (3 x 3 x 3)
Cube root = 2 x 2 x 2 x 2 x 3 = 48
(viii) Cube root of 46656:
Solution:
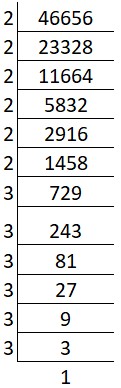
Prime factors of 46656 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 x 3 x 3 x 3
Group the factors in triples: ∛(2 x 2 x 2) x (2 x 2 x 2) x (3 x 3 x 3) x (3 x 3 x 3)
Cube root = 2 x 2 x 3 x 3 = 36
(ix) Cube root of 175616:
Solution:
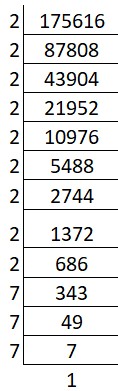
Prime factors of 175616 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 7 x 7 x 7
Group the factors in triples: ∛(2 x 2 x 2) x (2 x 2 x 2) x (2 x 2 x 2) x (7 x 7 x 7)
Cube root = 2 x 2 x 2 x 7 = 56
(x) Cube root of 91125:
Solution:
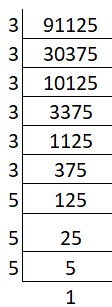
Prime factors of 91125 = 3 x 3 x 3 x 3 x 3 x 3 x 5 x 5 x 5
Group the factors in triples: (3 x 3 x 3) x (3 x 3 x 3) x (5 x 5 x 5)
Cube root = 3 x 3 x 5 = 45
2. State true or false.
(i) Cube of any odd number is even.
(ii) A perfect cube does not end with two zeros.
(iii) If square of a number ends with 5, then its cube ends with 25.
(iv) There is no perfect cube which ends with 8.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a two digit number may have seven or more digits.
(vii) The cube of a single digit number may be a single digit number.
Solution
(i) Cube of any odd number is even.
Ans: False.
Reason: The cube of an odd number remains odd. Example: 3³ = 27, which is odd.
(ii) A perfect cube does not end with two zeros.
Ans: True.
Reason: For a number to be a perfect cube and end with two zeros, it must have three zeros at the end.
(iii) If the square of a number ends with 5, then its cube ends with 25.
Ans: False.
Reason: The cube of a number ending in 5 ends in 125. Example: 5³ = 125.
(iv) There is no perfect cube which ends with 8.
Ans: False.
Reason: A perfect cube can end with 8. Example: 2³ = 8.
(v) The cube of a two-digit number may be a three-digit number.
Ans: True.
Example: 4³ = 64, a three-digit number.
(vi) The cube of a two-digit number may have seven or more digits.
Ans: False.
Reason: The cube of a two-digit number will have at most six digits. Example: 99³ = 970299, six digits.
(vii) The cube of a single-digit number may be a single-digit number.
Ans: True.
Example: 1³ = 1 and 2³ = 8, both single-digit numbers.