In Exercise 9.2 of the NCERT book of Class 8, we will solve the questions for the surface area of the cube, cuboid and cylinder. This may be tricky at times, but we will make it simple for you to solve.
Surface Area of Cube, Cuboid and Cylinder
Surface Area of Cube:
Formula: 6a²
Explanation: The surface area of a cube is six times the area of one of its faces (a²), since a cube has six identical square faces and ‘a’ represents the length of a side of the cube.
Surface Area of Cuboid:
Formula: 2(lw + lh + wh)
Explanation: The surface area of a cuboid is the sum of the areas of all its faces. Since a cuboid has opposite faces that are identical, the formula includes the area of the bottom and top (lw), front and back (lh), and left and right (wh) faces, all multiplied by 2.
Surface Area of Cylinder:
Formula: 2πr(r + h)
Explanation: The surface area of a cylinder includes the areas of the two circular bases (2πr²) and the lateral surface area (2πrh). ‘r’ is the radius of the base and ‘h’ is the height of the cylinder. The formula combines these two areas to cover the entire surface of the cylinder.
[joli-toc]
Exercise 9.2 Mensuration Quick Notes
Lets have a look at some of the formulas again in short and few examples.
- Surface Area of Cube:
- Formula: 6a²
- The surface area is six times the area of one face.
- Surface Area of Cuboid:
- Formula: 2(lw + lh + wh)
- Sum of areas of all faces.
- Surface Area of Cylinder:
- Formula: 2πr(r + h)
- Includes areas of two bases and lateral surface.
Example 1: Calculate the surface area of a cuboid with dimensions 4 cm, 3 cm, and 5 cm.
- Step 1: Identify the dimensions: l = 4 cm, w = 3 cm, h = 5 cm.
- Step 2: Use the formula 2(lw + lh + wh).
- Step 3: Calculate each product: lw = 4 × 3 = 12, lh = 4 × 5 = 20, wh = 3 × 5 = 15.
- Step 4: Sum the products: 12 + 20 + 15 = 47.
- Step 5: Multiply by 2: 2 × 47 = 94 cm².
Example 2: Find the surface area of a cylinder with radius 7 cm and height 10 cm.
- Step 1: Identify the radius and height: r = 7 cm, h = 10 cm.
- Step 2: Use the formula 2πr(r + h).
- Step 3: Calculate the inner sum: r + h = 7 + 10 = 17.
- Step 4: Multiply by the radius: r × 17 = 7 × 17 = 119.
- Step 5: Multiply by 2π: 2π × 119 ≈ 748 cm² (using π ≈ 3.14).
Example 3: Find the side length of a cube with surface area 486 cm².
- Step 1: Use the formula 6a² = 486.
- Step 2: Divide both sides by 6: a² = 81.
- Step 3: Take the square root of both sides: a = 9 cm.
Example 4: Calculate the surface area of a cuboid without the bottom with dimensions 8 cm, 6 cm, and 4 cm.
- Step 1: Identify the dimensions: l = 8 cm, w = 6 cm, h = 4 cm.
- Step 2: Calculate the total surface area using 2(lw + lh + wh): 2(48 + 32 + 24) = 208 cm².
- Step 3: Calculate the area of the bottom: lw = 48 cm².
- Step 4: Subtract the bottom area from the total surface area: 208 – 48 = 160 cm².
NCERT Solutions for Class 8 Maths Exercise 9.2 Chapter 9 Mensuration
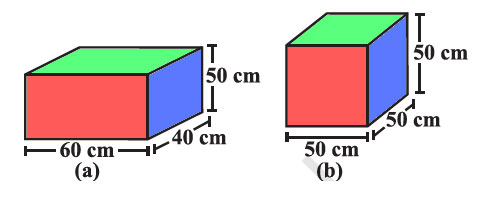
1. There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?
Solution
To determine which box requires less material, we are going to compare their surface areas.
For the first cuboidal box, given –
Length(l) = 60 cm
Breadth (b) = 40 cm
Height (h) = 50 cm
Total surface area of a cuboid = 2(lb + bh + hl)
2(60 × 40 + 40 × 50 + 50 × 60) (putting the value of l, b, h in the formula)
= 2(2400 + 2000 + 3000)
= 2 × 7400 = 14800 cm²
For the second cuboidal box, given –
Length(l) = 50 cm
Breadth (b) = 50 cm
Height (h) = 50 cm
Total surface area of a cuboid = 2(lb + bh + hl)
2(50 × 50 + 50 × 50 + 50 × 50) (putting the value of l, b, h in the formula)
= 2(2500 + 2500 + 2500)
= 2 × 7500 = 15000 cm²
The total surface area of the cuboidal box (a) is less, cuboidal box (a) would require less material to make. (Box with the smaller surface area requires less material.)
2. A suitcase with measures 80 cm × 48 cm × 24 cm is to be covered with a tarpaulin cloth. How many metres of tarpaulin of width 96 cm is required to cover 100 such suitcases?
Solution
For the suitcase, given –
Length(l) = 80 cm
Breadth (b) = 48 cm
Height (h) = 24 cm
Total surface area of a cuboid = 2(lb + bh + hl)
Surface area of one suitcase = 2(80 × 48 + 48 × 24 + 24 × 80) cm²
= 2(3840 + 1152 + 1920)
= 2 × 6912
= 13824 cm²
To cover 1 suitcase, area of tarpaulin cloth required will be = 13824 cm²
Given, width of the tarpaulin cloth = 96 cm
Area of tarpaulin cloth required to cover 1 suitcase = Total surface area of the suitcase
Area of tarpaulin cloth required to cover 1 suitcase = 13824 cm²
=) Length × Width = 13824 (since tarpaulin is in the form of rectange. Area of Rectangle = Length × Width)
=) Length × 96 = 13824
=) Length = 13824/96
= 144 cm
Length of tarpaulin cloth required to cover 100 suitcases = 100 × 144
= 144000 cm
= 144000/100 (converting centimeter to meter by dividing with 100)
= 144 m
A total of 144 m of tarpaulin cloth with width of 96 cm is required to cover 100 suitcases.
3. Find the side of a cube whose surface area is 600 cm².
Solution
Total surface area of a cube = 6 × side².
Given, total surface area of the cube is 600 cm²
600 cm² = 6 × side².
side² = 600/6
Solving for side, side = √(600/6)
= √100
= 10 cm
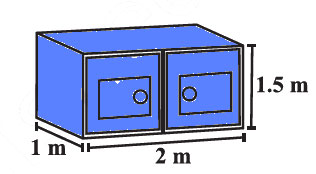
4. Rukhsar painted the outside of the cabinet of measure 1 m × 2 m × 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet.
Solution
Given the dimensions of the cabinet –
Length(l) = 1 m
Breadth (b) = 2 m
Height (h) = 1.5 m
The surface area of the painted cabinet = Total surface area of the cabinet – Area of the bottom
= 2(lb + bh + hl) – lb
= lb + 2bh + 2hl
= 2(1 × 2 + 2 × 2 × 1.5 + 2 × 1.5 × 1
= (2 + 6 + 3) m²
= 11 m²
Area of cabinet she covers is 11 m²
5. Daniel is painting the walls and ceiling of a cuboidal hall with length breadth and height of 15 m, 10 m, and 7 m respectively. From each can of paint 100 m² of area is painted. How many cans of paint will he need to paint the room?
Solution
Given the dimensions of the wall –
Length(l) = 15 m
Breadth (b) = 10 m
Height (h) = 7 m
Surface area of walls and ceiling to be painted = 2h(l + b) + l × b
= 2 × 7(15 + 10) + 15 × 10
= 2 × 7 × 25 + 150
= 350 + 150
= 500 m²
Each can can paint and area of 100 m²
Number of cans required for painting = Area to be painted/Area painted by 1 can
= 500 m²/100 m²
= 5
Daniel require 5 cans of paint to paint the hall
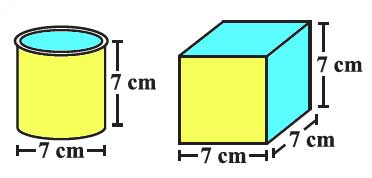
Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?
Solution
Similarities:
– Both figures have the same height of 7 cm.
– The diameter of the cylinder and the side length of the cube are both 7 cm.
Differences:
– The cylinder has a circular base while the cube has a square base.
– The cylinder’s lateral surface is curved while the cube’s lateral surface consists of four flat squares.
For the cylinder –
Diameter = 7 cm
Radius(r) = Diameter/2
= 7/2 cm
Height = 7 cm
Lateral Surface Area of the cube = 4 × side²
= 4 × (7 cm × 7 cm)
= 196 cm².
Curbed lateral Surface Area of the cylinder = 2πr × h
= 2 × 22/7 × 7/2 cm × 7 cm
= 154 cm².
The cube(2nd figure) has a larger lateral surface area than the cylinder.
7. A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How much sheet of metal is required?
Solution
The surface area of a cylinder includes the areas of its two circular ends and its lateral surface.
Surface area = 2πr² (ends) + 2πrh (lateral surface).
Given, for radius of the cylinder(r) = 7 m and Height (h) = 3 m:
Surface area = 2 × 22/7 × 7² + 2 × 22/7 × 7 × 3
= 2 × 22 × 7 + 2 × 22 × 3
= 308 + 132
= 440 m²
440 m² sheet of metal is required to build a closed cylindrical tank
8. The lateral surface area of a hollow cylinder is 4224 cm². It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of the rectangular sheet?
Solution
When we cut the hollow cylinder along its height, we get a rectangular sheet of width 33 cm. This is height of the cylinder.
Here we can assume radius of the hollow cylinder be r
Lateral surface area of the cylinder = length of the rectangle × width of the rectangle.
For a lateral surface area of 4224 cm² and a width of 33 cm:
Lateral surface area of the cylinder = 2πrh
4224 = 2πrh (since, Lateral surface area = 4224)
2 × 22/7 × r × 33 = 4224
r = 4224 × 7/(2 × 22 × 33)
= (7 × 96)/33
= (7 × 33)/11
= 21 cm
On cutting the hollow cylinder, the base’s perimeter is equal to length of rectangular sheet
Length of the rectangle = Perimeter of circular base
Perimeter of circular base = 2πr
= 2 × 22/7 × 21
= 128 cm.
Perimeter of the rectangle = 2 × (length + width)
= 2 × (128 cm + 33 cm) = 2 × 161 cm = 322 cm
The perimeter of rectangular sheet is 322 cm
9. A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1 m.

Hint: The road roller is in the shape of a cylinder. The area covered by the roller will be equal to curved surface area of the roller.
Solution
Given –
Length of the roller = 1 m = 100 cm
Diameter of road roller = 84 cm
Radius of road roller = 84/2 = 42 cm
Curved surface area of the cylinder = 2πrh
= 2 × 22/7 × 42 × 100
= 26400 cm²
Area covered by the road roller in one revolution = Curved surface area of the roller
= 26400 cm² (lets conver it to m²)
= 26400/(100 × 100)
= 2.64 m²
Area covered by road roller in 750 revolutions = 750 × 2.64
= 1980 m² is the required area of the road
10. A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom what is the area of the label.
Solution
The label covers the lateral surface area of the cylinder, minus the top and bottom 2 cm.
Radius of the cylinder, r = 14/2 cm = 7 cm.
Effective height of the label, h = 20 cm – 2 cm – 2 cm = 16 cm.
Lateral surface area for the label = 2πrh = 2 × π × 7 cm × 16 cm = 2 × 3.14 × 7 × 16 cm² = 704 cm².
Therefore, the area of the label is 704 cm².
Extra Challenging MCQ Questions for Exercise 9.2 Mensuration Chapter 9
1. A cube has a surface area of 150 cm². What is the length of each side?
a) 5 cm
b) 6 cm
c) 7 cm
d) 8 cm
Answer:
a) 5 cm
Hint: Surface area of a cube = 6a²
2. The surface area of a cuboid is 94 cm², with dimensions 4 cm x 3 cm x h cm. What is the height (h) of the cuboid?
a) 5 cm
b) 6 cm
c) 7 cm
d) 8 cm
Answer:
a) 5 cm
Hint: Surface area of a cuboid = 2(lw + lh + wh)
3. A cylinder has a surface area of 462 cm² and a height of 7 cm. What is the radius of its base? (Use π = 22/7)
a) 3 cm
b) 5 cm
c) 7 cm
d) 9 cm
Answer:
b) 5 cm
Hint: Surface area of a cylinder = 2πr(r + h)
4. If the side length of a cube is doubled, how does its surface area change?
a) It doubles
b) It triples
c) It quadruples
d) It remains the same
Answer:
c) It quadruples
Hint: Surface area is proportional to the square of the side length.
5. A cuboid has a surface area of 214 cm² with dimensions 5 cm x 4 cm x h cm. What is the height (h) of the cuboid?
a) 6 cm
b) 7 cm
c) 8 cm
d) 9 cm
Answer:
b) 7 cm
Hint: Surface area of a cuboid = 2(lw + lh + wh)
6. The lateral surface area of a cylinder is 132 cm², and its height is 6 cm. What is the radius of its base? (Use π = 22/7)
a) 2 cm
b) 3 cm
c) 4 cm
d) 5 cm
Answer:
d) 5 cm
Hint: Lateral surface area of a cylinder = 2πrh
7. A cube and a cuboid have the same surface area. If the cube’s side length is 6 cm and the cuboid’s dimensions are 4 cm x 5 cm x h cm, what is the height (h) of the cuboid?
a) 6 cm
b) 7 cm
c) 8 cm
d) 9 cm
Answer:
a) 6 cm
Hint: Equate the surface areas: 6a² = 2(lw + lh + wh)
8. The surface area of a cylinder is 616 cm², and its radius is 7 cm. What is its height? (Use π = 22/7)
a) 8 cm
b) 10 cm
c) 12 cm
d) 14 cm
Answer:
a) 8 cm
Hint: Surface area of a cylinder = 2πr(r + h)
9. A cuboid has a surface area of 130 cm² with dimensions 5 cm x w cm x 3 cm. What is the width (w) of the cuboid?
a) 4 cm
b) 5 cm
c) 6 cm
d) 7 cm
Answer:
c) 6 cm
Hint: Surface area of a cuboid = 2(lw + lh + wh)
10. If the radius and height of a cylinder are both doubled, how does its surface area change?
a) It doubles
b) It triples
c) It quadruples
d) It remains the same
Answer:
c) It quadruples
Hint: Surface area is proportional to the square of the dimensions.
Practice Worksheet with Challenging Questions For Class 8 Exercise 9.2 Mensuration
Questions
- A cylindrical pillar with a radius of 5 m and a height of 10 m is painted on the outside. What is the cost of painting it at ₹50 per m²?
- Calculate the volume of a cone with a radius of 7 cm and a height of 24 cm.
- Find the total surface area of a sphere with a diameter of 14 cm.
- A water tank is in the shape of a cylinder with a diameter of 6 m and a height of 10 m. Find its capacity in liters.
- A rectangular sheet of paper 44 cm by 18 cm is rolled along its length to form a cylinder. Find the volume of the cylinder.
- Find the height of a cylinder whose volume is 1232 cm³ and the radius of the base is 7 cm.
- A cube’s volume is 512 cm³. Find the length of its diagonal.
- Find the area of a trapezium with parallel sides measuring 20 cm and 15 cm, and the distance between them is 7 cm.
- Calculate the lateral surface area of a pyramid with a square base of side 10 m and a slant height of 15 m.
- A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical bottles of radius 3 cm and height 4 cm. How many bottles are required to empty the bowl?
- A cuboidal room is 6 m long, 5 m wide, and 4 m high. Find the cost of whitewashing the walls and ceiling at ₹20 per m².
- A garden roller in the shape of a cylinder has a width of 1.5 m and a diameter of 70 cm. How many times must it roll to level a garden 75 m long and 30 m wide?
- The base of a right prism is a triangle with sides 5 cm, 12 cm, and 13 cm. If the height of the prism is 10 cm, find its volume.
- A cone and a hemisphere have equal bases with a radius of 7 cm. If the height of the cone is 24 cm, find the total volume of the combined solid.
- A solid is in the shape of a cylinder with hemispherical ends. The total height of the solid is 28 cm and the diameter of the cylinder is 14 cm. Calculate the total volume of the solid.
Answers
- ₹7850 (Calculate the lateral surface area of the cylinder and multiply by the cost per m²)
- 1232 cm³ (Volume of a cone)
- 616 cm² (Total surface area of a sphere)
- 282.74 cubic meters or 282740 liters (Calculate the volume and convert to liters)
- 2826 cm³ (Find the radius of the cylinder from the width of the paper and calculate the volume)
- 8 cm (Volume of a cylinder)
- 12 cm (Use the diagonal formula for a cube)
- 245 cm² (Area of a trapezium formula)
- 600 m² (Lateral surface area of the pyramid)
- 38 bottles (Volume of the bowl and the bottle, then divide)
- ₹880 (Calculate the total area to be whitewashed and multiply by the cost per m²)
- 133 times (Area covered in one revolution and then find the number of revolutions)
- 300 cm³ (Volume of a prism)
- 2058.12 cm³ (Volumes of the cone and hemisphere)
- 4312 cm³ (Volumes of the cylinder and hemispheres and add them up)